题目内容
【题目】如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
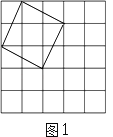
（1）在图1中以格点为顶点画一个面积为5的正方形； 
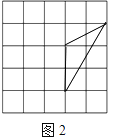
（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、 
、 
； 
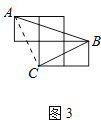
（3）如图3，A、B、C是小正方形的顶点，求∠ABC． 
【答案】
（1）解：如图所示：
（2）解：如图所示：
（3）解：连接AC，
由勾股定理得：AC=BC= 
，AB= 
，
∵AC2+BC2=AB2=10，
∴△ABC为等腰直角三角形
∴∠ABC=45°
【解析】（1）面积为5的正方形的边长为 ，画出正方形即可；（2）以直角边为1和2构造斜边为 ，再以2和3为直角边构造斜边为 
就得到三角形三边长分别为2、 、 ；（3）连接AC，利用勾股定理的逆定理证明△ACB为直角三角形即可得到∠ABC的度数．
阅读快车系列答案【题目】一件进价为100元的商品，先按进价提高20%作为标价，但因销量不好，又决定按标价降价20%出售。那么这次生意的盈亏情况是每件（ ）
A. 不亏不赚 B. 亏了4元 C. 赚了4元 D. 赚了6元
【题目】甲、乙、丙、丁四个小组的同学分别参加了班里组织的中华古诗词知识竞赛，在相同条件下各小组的成绩如下表所示，若要从中选择一个小组参加年级的比赛，那么应选（ ）
甲组 | 乙组 | 丙组 | 丁组 | |
平均分 | 85 | 90 | 88 | 90 |
方差 | 3.5 | 3.5 | 4 | 4.2 |
A. 甲组B. 乙组C. 丙组D. 丁组
【题目】某工厂计划生产A，B两种产品共10件，其生产成本和利润如下表：
A种产品 | B种产品 | |
成本（万元/件） | 2 | 5 |
利润（万元/件） | 1 | 3 |
（1）若工厂计划获利14万元，问A，B两种产品应分别生产多少件？
（2）若工厂计划投入资金不多于44万元，且获利多于14万元，问工厂有哪几种生产方案？
（3）在（2）的条件下，哪种生产方案获利最大？并求出最大利润．
