题目内容
.如图,在平面直角坐标系中,函数 (x>0,常数k>0)
(x>0,常数k>0)
的图象经过点A(1,2)、B(m,n)(m>1).过点B作y轴的垂线,
垂足为C若△ABC的面积为2,则点B的坐标为________.
 (x>0,常数k>0)
(x>0,常数k>0)的图象经过点A(1,2)、B(m,n)(m>1).过点B作y轴的垂线,
垂足为C若△ABC的面积为2,则点B的坐标为________.

分析:由于函数
 (x>0常数k>0)的图象经过点A(1,2),把(1,2)代入解析式即可确定k=2,依题意BC=m,BC边上的高是2-n="2-"
(x>0常数k>0)的图象经过点A(1,2),把(1,2)代入解析式即可确定k=2,依题意BC=m,BC边上的高是2-n="2-"  ,根据三角形的面积公式得到关于m的方程,解方程即可求出m,然后把m的值代入y=
,根据三角形的面积公式得到关于m的方程,解方程即可求出m,然后把m的值代入y=  ,即可求得B的纵坐标,最后就求出点B的坐标.
,即可求得B的纵坐标,最后就求出点B的坐标.解:∵函数
 (x>0常数k>0)的图象经过点A(1,2),
(x>0常数k>0)的图象经过点A(1,2),∴把(1,2)代入解析式得2=
 ,
,∴k=2,

∵B(m,n)(m>1),
∴BC=m,当x=m时,n=
 ,
,∴BC边上的高是2-n=2-
 ,
,而S△ABC=
 m(2-
m(2- )=2,
)=2,∴m=3,
∴把m=3代入y=
 ,
,∴n=
 ,
,∴点B的坐标是(3,
 ).
).故填空答案:(3,
 ).
).
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
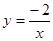
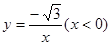



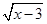 中,自变量x的取值范围是________________
中,自变量x的取值范围是________________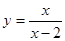 中自变量
中自变量 的取值范围是 ▲ .
的取值范围是 ▲ . 中,自变量
中,自变量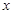 的取值范围是( ▲ )
的取值范围是( ▲ )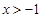
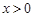
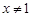
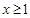
 .
.