题目内容
(7分)某市“全国文明村”白村果农王保收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王保如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王保应选择哪种方案,使运输费最少?最少运费是多少?
(1)王保如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王保应选择哪种方案,使运输费最少?最少运费是多少?
(1)设安排甲种货车x辆,则安排乙种货车(8-x)辆,依题意,得
4x+2(8-x)≥20,且x+2(8-x)≥12,
解此不等式组,得x≥2,且x≤4,即2≤x≤4.
∵x是正整数,
∴x可取的值为2,3,4.
因此安排甲、乙两种货车有三种方案:
| | 甲种货车 | 乙种货车 |
| 方案一 | 2辆 | 6辆 |
| 方案二 | 3辆 | 5辆 |
| 方案三 | 4辆 | 4辆 |
方案三所需运费300×4+240×4=2160元.
所以王保应选择方案一运费最少,最少运费是2040元.
试题考查知识点:利用不等式组解应用题
思路分析:抽取关系列不等式组
具体解答过程:
(1)设安排甲种货车x辆,则安排乙种货车(8-x)辆,依题意,得:
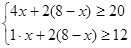
解之得:
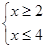 即2≤x≤4
即2≤x≤4∵车辆数x只能为正整数
∴x=2,3,4
因此安排甲、乙两种货车有三种方案:
| | 甲种货车 | 乙种货车 |
| 方案一 | 2辆 | 6辆 |
| 方案二 | 3辆 | 5辆 |
| 方案三 | 4辆 | 4辆 |
方案一:甲种货车2辆、乙种货车6辆:运费为300×2+240×6=2040元;
方案二:甲种货车3辆、乙种货车5辆:运费为300×3+240×5=2100元;
方案三:甲种货车4辆、乙种货车4辆:运费为300×4+240×4=2160元;
三种方案所需运费比较可知,方案一的运费最少,最少运费是2040元。
答:(略)
试题点评:应用题的结果往往要符合现实意义,不等式组可以把所有可能的结果呈现出来。

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 (x>0,常数k>0)
(x>0,常数k>0) (升)与行驶时间
(升)与行驶时间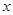 (时)之间的关系:
(时)之间的关系: (升)
(升)

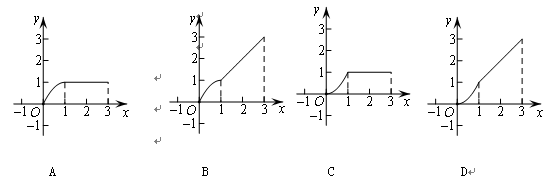

 .
. 的图象( ▲ )
的图象( ▲ )