题目内容
【题目】如图,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,与y轴交于点
,与y轴交于点![]() ,与x轴交于点C.
,与x轴交于点C.
![]() 求直线
求直线![]() 的函数表达式;
的函数表达式;
![]() 求
求![]() 的面积;
的面积;
![]() 在平面直角坐标系中有一点
在平面直角坐标系中有一点![]() ,使得
,使得![]() ,请求出点P的坐标;
,请求出点P的坐标;
![]() 点M为直线
点M为直线![]() 上的动点,过点M作y轴的平行线,交
上的动点,过点M作y轴的平行线,交![]() 于点N,点Q为y轴上一动点,且
于点N,点Q为y轴上一动点,且![]() 为等腰直角三角形,请直接写出满足条件的点M的坐标.
为等腰直角三角形,请直接写出满足条件的点M的坐标.

【答案】(1)y=-2x+6;(2)3;(3)(5,2)或(5,8);(4)![]() 或
或![]() 或(6,-6) 或(3,0).
或(6,-6) 或(3,0).
【解析】
![]() 先求点A坐标,再用待定系数法求函数解析式.
先求点A坐标,再用待定系数法求函数解析式.
![]() 求点C坐标,以OC为底,点A到x轴距离为高计算.
求点C坐标,以OC为底,点A到x轴距离为高计算.
![]() 观察面积相等两个三角形,有公共边OA,故可看作是以OA为底,高相等
观察面积相等两个三角形,有公共边OA,故可看作是以OA为底,高相等![]() 所以点P在与OA平行的直线上,且到直线OA距离等于点C到OA距离
所以点P在与OA平行的直线上,且到直线OA距离等于点C到OA距离![]() 其中一条即为过点C的直线,根据平移,另一条经过点C关于A的对称点
其中一条即为过点C的直线,根据平移,另一条经过点C关于A的对称点![]() 求出直线后,把
求出直线后,把![]() 代入即求出点P坐标.
代入即求出点P坐标.
![]() 由于直角不确定,需分类讨论,得到MN与M的横坐标的关系
由于直角不确定,需分类讨论,得到MN与M的横坐标的关系![]() 列得方程求解即可.
列得方程求解即可.
解:![]() 点
点![]() 在直线
在直线![]() :
:![]() 上,
上,
![]() ,即
,即![]() ,
,
![]() 直线
直线![]() :
:![]() 过点
过点![]() 、点
、点![]() ,
,
![]() 解得:
解得:![]() ,
,
![]() 直线直线
直线直线![]() 的函数表达式为:
的函数表达式为:![]() ;
;
![]() 令
令![]() ,解得:
,解得:![]() ,
,
![]() 点
点![]() 即
即![]() ,
,
![]() ,
,
![]() ,
,
![]() 当以AO为底边时,两三角形等高,
当以AO为底边时,两三角形等高,
![]() 过点P且与直线AO平行的直线
过点P且与直线AO平行的直线![]() 为:
为:![]() ,
,
![]() 直线
直线![]() 过点
过点![]() ,得
,得![]() 为:
为:![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点
点![]() ,
,
![]() 点
点![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,
,
直线![]() 过点
过点![]() ,得
,得![]() 为:
为:![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 点
点![]()
综上所述,点P坐标为![]() 或
或![]()
![]() 设
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() 如图1,若
如图1,若![]() ,
,![]() ,
,

则有![]() ,
,
![]() ,
,
![]() 或
或![]() ,
,
![]() 或
或![]() ,
,
![]() 如图2,图3,若
如图2,图3,若![]() 或
或![]() ,
,
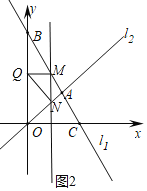

则![]() ,
,
![]() ,
,
![]() 或
或![]() ,
,
![]() 或
或![]()
综上所述,点M的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目