题目内容
如图,在Rt△ABC中,∠C=90°,AD是∠CAB的平分线,tanB=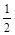 ,则CD∶DB =
,则CD∶DB = 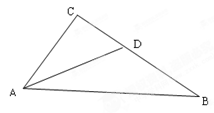
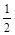 ,则CD∶DB =
,则CD∶DB = 
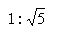
作出DE⊥AB,根据角平分线的性质得出CD=DE,进一步得出CD:BD=DE:BD,再利用tanB=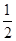 ,得出
,得出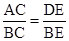 =
=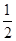 ,从而利用勾股定理求出.
,从而利用勾股定理求出.
解答: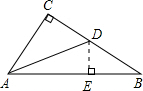 解;过点D作DE⊥AB,垂足为E,
解;过点D作DE⊥AB,垂足为E,
∵AD是∠CAB 的平分线,
∴∠CAD=∠DAB,
∵∠C=90°,DE⊥AB,
∴CD=DE,
∴CD:BD=DE:BD,
∵tanB=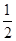 ,
,
∴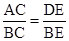 =
=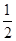 ,
,
∴DE=x,BE=2x,BD=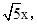
CD:BD=1: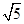 ,
,
故答案为:1: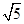 .
.
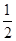 ,得出
,得出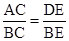 =
=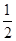 ,从而利用勾股定理求出.
,从而利用勾股定理求出.解答:
 解;过点D作DE⊥AB,垂足为E,
解;过点D作DE⊥AB,垂足为E,∵AD是∠CAB 的平分线,
∴∠CAD=∠DAB,
∵∠C=90°,DE⊥AB,
∴CD=DE,
∴CD:BD=DE:BD,
∵tanB=
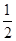 ,
,∴
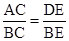 =
=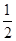 ,
,∴DE=x,BE=2x,BD=
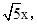
CD:BD=1:
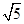 ,
,故答案为:1:
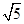 .
.
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

 (2)
(2) 

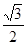

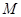 、
、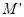 、
、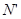 、
、 .小明在探究线段
.小明在探究线段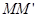 与
与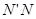 的数量关系时,从点
的数量关系时,从点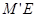 、
、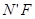 ,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题:
,利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题: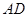 、
、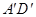 、
、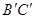 、
、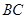 于
于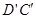 、
、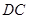 于
于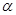 ,你认为
,你认为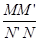 的值(用含
的值(用含
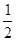

 .
.