��Ŀ����
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P��a��b��������P�������Ϊ��![]() ��ka+b��������kΪ��������k��0������Ƶ�P��Ϊ��P�ġ�k�������㡱��
��ka+b��������kΪ��������k��0������Ƶ�P��Ϊ��P�ġ�k�������㡱��
���磺P��1��4���ġ�2�������㡱ΪP�䣨1+![]() ��2��1+4������P�䣨3��6����
��2��1+4������P�䣨3��6����
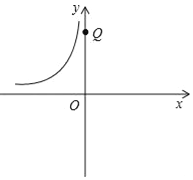
��1���ٵ�P����1����2���ġ�2�������㡱P�������Ϊ _________ ��
������P�ġ�k�������㡱P�������Ϊ��3��3������д��һ�����������ĵ�P������_________ ��
��2������P��x����������ϣ���P�ġ�k�������㡱ΪP��㣬�ҡ�OPP��Ϊ����ֱ�������Σ���k��ֵ��
���𰸡���1������2����4������1��2����2����1
��������
�����������1����ֻ���a=��1��b=��2��k=2���루![]() ��ka+b���������P������꣮
��ka+b���������P������꣮
����P�䣨3��3�������k=1���Ӷ���a+b=3����ȡһ��a�Ϳ������Ӧ��b���Ӷ��õ����������ĵ�P��һ�����꣮
��2�����P����Ϊ��a��0�����Ӷ���P�䣨a��ka������ȻPP���OP���������ɵ�OP=PP�䣬�Ӷ����k��
�����������1���ٵ�a=��1��b=��2��k=2ʱ��
��![]() =��1+
=��1+![]() =��2��ka+b=2������1����2=��4��
=��2��ka+b=2������1����2=��4��
���P����1����2���ġ�2�������㡱P�������Ϊ����2����4����
�ʴ�Ϊ������2����4����
������ɵã�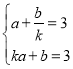 ��
��
��ka+b=3k=3��
��k=1��
��a+b=3��
��b=3��a��
��a=1ʱ��b=2����ʱ��P������Ϊ��1��2����
�ʴ�Ϊ����1��2����
˵����ֻҪ��P�ĺ�������������ĺ͵���3���ɣ�
��2���ߵ�P��x����������ϣ�
��b=0��a��0��
���P��������a��0������P���������a��ka����
��PP���OP��
�ߡ�OPP��Ϊ����ֱ�������Σ�
��OP=PP�䣮
��a=��ka��
��a��0��
��k=��1��
�ʴ�Ϊ����1��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�