题目内容
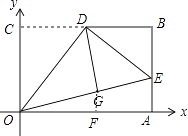
【题目】如图,在平面直角坐标系xOy中,矩形OABC的边OA、OC分别在x轴和y轴上,OC=3,OA=2 ![]() ,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 .
,D是BC的中点,将△OCD沿直线OD折叠后得到△OGD,延长OG交AB于点E,连接DE,则点G的坐标为 . 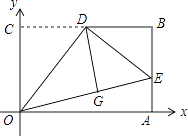
【答案】( ![]() ,
, ![]() )
)
【解析】解:过点G作GF⊥OA于点F,如图所示.
∵点D为BC的中点,
∴DC=DB=DG,
∵四边形OABC是矩形,
∴AB=OC,OA=BC,∠C=∠OGD=∠ABC=90°.
在Rt△DGE和Rt△DBE中, ![]() ,
,
∴Rt△DGE≌Rt△DBE(HL),
∴BE=GE.
设AE=a,则BE=3﹣a,DE= ![]() =
= ![]() ,OG=OC=3,
,OG=OC=3,
∴OE=OG++GE,即 ![]() =3+3﹣a,
=3+3﹣a,
解得:a=1,
∴AE=1,OE=5.
∵GF⊥OA,EA⊥OA,
∴GF∥EA,
∴ ![]() ,
,
∴OF= ![]() =
= ![]() =
= ![]() ,GF=
,GF= ![]() =
= ![]() =
= ![]() ,
,
∴点G的坐标为( ![]() ,
, ![]() ).
).
故答案为:( ![]() ,
, ![]() ).
).
本题考查了翻折变换、矩形的性质、全等三角形的判定及性质以及平行线的性质,解题的关键是求出线段AE的长度.本题属于中档题,难度不大,解决该题型题目时,利用勾股定理得出边与边之间的关系是关键.过点G作GF⊥OA于点F,根据全等直角三角形的判定定理(HL)证出Rt△DGE≌Rt△DBE,从而得出BE=GE,根据勾股定理可列出关于AE长度的方程,解方程可得出AE的长度,再根据平行线的性质即可得出比例关系 ![]() ,代入数据即可求出点G的坐标.
,代入数据即可求出点G的坐标.

练习册系列答案
相关题目