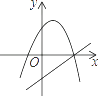题目内容
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),( ![]() ,y2)是抛物线上两点,则y1>y2 . 其中说法正确的是 .
,y2)是抛物线上两点,则y1>y2 . 其中说法正确的是 . 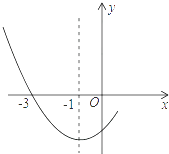
【答案】①②④
【解析】解:①∵二次函数的图象开口向上,
∴a>0,
∵二次函数的图象交y轴的负半轴于一点,
∴c<0,
∵对称轴是直线x=﹣1,
∴﹣ ![]() =﹣1,
=﹣1,
∴b=2a>0,
∴abc<0,
故①正确;
②∵b=2a,
∴2a﹣b=0,
故②正确;
③∵抛物线的对称轴为x=﹣1,且过点(﹣3,0),
∴抛物线与x轴另一交点为(1,0).
∵当x>﹣1时,y随x的增大而增大,
∴当x=2时y>0,即4a+2b+c>0,
故③错误;
④∵(﹣5,y1)关于直线x=﹣1的对称点的坐标是(3,y1),
又∵当x>﹣1时,y随x的增大而增大,3> ![]() ,
,
∴y1>y2 ,
故④正确;
故答案为:①②④.
根据抛物线开口方向得到a>0,根据抛物线的对称轴得b=2a>0,则2a-b=0,则可对②进行判断;根据抛物线与y轴的交点在x轴下方得到c<0,则abc<0,于是可对①进行判断;由于x=-2时,y<0,则得到4a-2b+c<0,则可对③进行判断;通过点(-5,y1)和点(2,y2)离对称轴的远近对④进行判断.

练习册系列答案
相关题目
【题目】曲靖市某商场投入19200元资金购进甲、乙两种饮料共600箱,饮料的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 36 | 52 |
(1)该商场购进甲、乙两种饮料各多少箱?
(2)全部售完600箱饮料,该商场共获得利润多少元?