题目内容
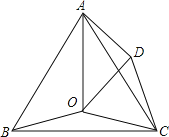
【题目】如图,O是等边三角形ABC内一点,∠AOB=110°,∠BOC=m°,D是△ABC外一点,且△ADC≌△BOC,连接OD.当m为_____时,△AOD是等腰三角形.
【答案】110或125或140.
【解析】
根据全等三角形的性质得到∠OCB=∠DCA,CO=CD,证明∠DCA+∠ACO=60°,根据等边三角形的判定定理证明△COD是等边三角形,然后分AD=AO、DA=DO、OD=AO三种情况,根据等腰三角形的性质,三角形内角和定理计算.
∵△ADC≌△BOC,
∴∠ADC=∠BOC=m°,∠OCB=∠DCA,CO=CD,
∵△ABC是等边三角形,
∴∠ACB=60°,即∠OCB+∠ACO=60°,
∴∠DCA+∠ACO=60°,又CO=CD,
∴△COD是等边三角形,
∴∠COD=∠CDO=60°;
∴∠AOD=360°-∠AOB-∠BOC-∠COD=360°-110°-m°-60°=190°-m°,
∠ADO=∠ADC-∠CDO=m°-60°,
∴∠OAD=180°-∠AOD-∠ADO=180°-(m°-60°)-(190°-m°)=50°,
若AD=AO,则∠ADO=∠AOD,即m°-60°=190°-m°,
解得:m°=125°;
若OA=OD,则∠ADO=∠OAD,则m°-60°=50°,
解得:m°=110°;
若DA=DO,则∠OAD=∠AOD,即50°=190°-m°,
解得:m°=140°;
综上所述,当m为125或110或140时,△AOD是等腰三角形,
故答案为110或125或140.

【题目】为了促进节能减排,倡导节约用电,某市将实行居民生活用电阶梯电价方案,图中折线反映了每户每月用电电费y(元)与用电量x(度)间的函数关系式.
(1)根据图象,阶梯电价方案分为三个档次,填写下表:
档次 | 第一档 | 第二档 | 第三档 |
每月用电量x(度) | 0<x≤140 |
(2)小明家某月用电120度,需交电费 元
(3)求第二档每月电费y(元)与用电量x(度)之间的函数关系式;
(4)在每月用电量超过230度时,每多用1度电要比第二档多付电费m元,小刚家某月用电290度,交电费153元,求m的值.