题目内容
(2009•房山区一模)已知关于x的一元二次方程kx2+(3k+1)x+2k+1=0.(1)求证:该方程必有两个实数根;
(2)设方程的两个实数根分别是x1,x2,若y1是关于x的函数,且y1=mx-1,其中m=x1x2,求这个函数的解析式;
(3)设y2=kx2+(3k+1)x+2k+1,若该一元二次方程只有整数根,且k是小于0的整数.结合函数的图象回答:当自变量x满足什么条件时,y2>y1?
【答案】分析:(1)用根的判别式判断根的情况;
(2)用一元二次方程根与系数的关系,可以求出关于y1解析式;
(3)根据已知方程只有整数根且k是小于0的整数确定出k的值,进而确定两个函数的解析式,求出两个函数的交点坐标,在坐标系中画出图象,再确定出y2>y1时的x的取值范围.
解答:(1)证明:∵a=k,b=3k+1,c=2k+1,
∴△=b2-4ac
=9k2+6k+1-4k(2k+1)
=9k2+6k+1-8k2-4k=k2+2k+1
=(k+1)2≥0,
∴方程必有两个实数根;
(2)解:∵方程的两个实数根分别是x1,x2,
∴x1x2= ,
,
而m=x1x2,y1=mx-1,
∴ ;
;
(3)解:∵方程只有整数根且k是小于0的整数,
∴ 要为整数,只能
要为整数,只能 为整数,
为整数,
∴k=-1,
∴y2=-x2-2x-1,y1=x-1,
∴y1与y2的交点坐标为A(-3,-4)B(0,-1),
∴在坐标系中画出两函数的图象如图所示,
由图象可知:
当-3<x<0时,y2>y1.
点评:本题有一定的难度,先用到一元二次方程的根的判别式和根与系数的关系来确定方程有根和函数的解析式,再求出了两函数的交点坐标,从而在坐标系中画出图象,确定出x的取值范围.
(2)用一元二次方程根与系数的关系,可以求出关于y1解析式;
(3)根据已知方程只有整数根且k是小于0的整数确定出k的值,进而确定两个函数的解析式,求出两个函数的交点坐标,在坐标系中画出图象,再确定出y2>y1时的x的取值范围.
解答:(1)证明:∵a=k,b=3k+1,c=2k+1,
∴△=b2-4ac
=9k2+6k+1-4k(2k+1)
=9k2+6k+1-8k2-4k=k2+2k+1
=(k+1)2≥0,
∴方程必有两个实数根;
(2)解:∵方程的两个实数根分别是x1,x2,

∴x1x2=
 ,
,而m=x1x2,y1=mx-1,
∴
 ;
;(3)解:∵方程只有整数根且k是小于0的整数,
∴
 要为整数,只能
要为整数,只能 为整数,
为整数,∴k=-1,
∴y2=-x2-2x-1,y1=x-1,
∴y1与y2的交点坐标为A(-3,-4)B(0,-1),
∴在坐标系中画出两函数的图象如图所示,
由图象可知:
当-3<x<0时,y2>y1.
点评:本题有一定的难度,先用到一元二次方程的根的判别式和根与系数的关系来确定方程有根和函数的解析式,再求出了两函数的交点坐标,从而在坐标系中画出图象,确定出x的取值范围.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 ,且图象向右平移一个单位后经过坐标原点O.
,且图象向右平移一个单位后经过坐标原点O.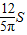 ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.
 的值.
的值.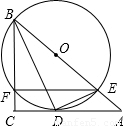
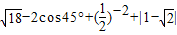 .
.