题目内容
(2009•房山区一模)已知:如图,在△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,DE⊥DB交AB于点E,过B、D、E三点作⊙O.(1)求证:AC是⊙O的切线;
(2)设⊙O交BC于点F,连接EF,若BC=9,CA=12.求
 的值.
的值.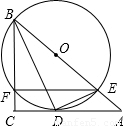
【答案】分析:(1)要想证明AC是切线,需要先连接OD,利用“经过半径的外端并且垂直于半径的直线是圆的切线”来证明AC是⊙O的切线,所以需要根据∠OBD=∠ODB,∠CBD=∠ABD,求得BC∥OD从而得到OD⊥AC;
(2)先利用△ADO∽△ACB求出半径r的值,再利用△BEF∽△BAC的相似比即可求出 的值为
的值为 .
.
解答: (1)证明:连接OD,
(1)证明:连接OD,
∵DE⊥DB,∴∠BDE=90°.
∴BE是⊙O的直径.
∵OB=OD,∴∠OBD=∠ODB.
∵BD平分∠ABC,∴∠CBD=∠ABD.
∴∠CBD=∠ODB.
∴BC∥OD.
∵∠ACB=90°,
∴BC⊥AC.
∴OD⊥AC.(1分)
∵OD是⊙O的半径,
∴AC是⊙O的切线.(2分)
(2)解:设⊙O的半径为r,
在△ABC中,∠ACB=90°,BC=9,CA=12,
∴AB=15.(3分)
∵BC∥OD,
∴△ADO∽△ACB.
∴ ,
,
∴ ,
,
∴ ,
,
∴ ,(4分)
,(4分)
又∵BE是⊙O的直径,
∴∠BEF=90°,
∴△BEF∽△BAC,
∴ .(5分)
.(5分)
点评:主要考查了角平分线的性质和切线的判定以及相似三角形中的成比例线段的运用.要掌握角平分线的性质和切线的判定,要会灵活运用相似中的成比例线段某条线段的长度或比值.
(2)先利用△ADO∽△ACB求出半径r的值,再利用△BEF∽△BAC的相似比即可求出
 的值为
的值为 .
.解答:
 (1)证明:连接OD,
(1)证明:连接OD,∵DE⊥DB,∴∠BDE=90°.
∴BE是⊙O的直径.
∵OB=OD,∴∠OBD=∠ODB.
∵BD平分∠ABC,∴∠CBD=∠ABD.
∴∠CBD=∠ODB.
∴BC∥OD.
∵∠ACB=90°,
∴BC⊥AC.
∴OD⊥AC.(1分)
∵OD是⊙O的半径,
∴AC是⊙O的切线.(2分)
(2)解:设⊙O的半径为r,
在△ABC中,∠ACB=90°,BC=9,CA=12,
∴AB=15.(3分)
∵BC∥OD,
∴△ADO∽△ACB.
∴
 ,
,∴
 ,
,∴
 ,
,∴
 ,(4分)
,(4分)又∵BE是⊙O的直径,
∴∠BEF=90°,
∴△BEF∽△BAC,
∴
 .(5分)
.(5分)点评:主要考查了角平分线的性质和切线的判定以及相似三角形中的成比例线段的运用.要掌握角平分线的性质和切线的判定,要会灵活运用相似中的成比例线段某条线段的长度或比值.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
 ,且图象向右平移一个单位后经过坐标原点O.
,且图象向右平移一个单位后经过坐标原点O.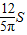 ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.
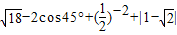 .
.