题目内容
若直线y=2x-1与y=x-k的交点在第四象限，则k的取值范围为 ________．
＜k＜1分析：可由已知y=2x-1与y=x-k求出其交点M为（1-k，1-2k），再根据交点在第四象限确定k的取值范围．
解答：直线y=2x-1与y=x-k的交点M为
M（1-k，1-2k）
该点在第四象限，则
1-k＞0，1-2k＜0
解不等式得：
＜k＜1．故答案为：
＜k＜1．点评：此题考查的知识点是两条直线相交问题，关键是先求出交点，再根据条件确定k的取值范围．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若直线y=2x-1与反比例函数y=
的图象交于点P（2，a），则反比例函数y=
的图象还必过点（ ）
| k |
| x |
| k |
| x |
| A、（-1，6） |
| B、（1，-6） |
| C、（-2，-3） |
| D、（2，12） |
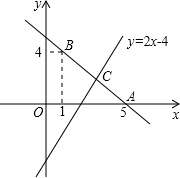如图，直线y=kx+b经过点A（0，5），B（1，4）．