题目内容
某汽车从A地驶向B地,若每分钟行驶a千米,则11点到达,若每分钟行驶 a千米,则11:20时距离B地还有10千米;如果改变出发时间,若每分钟行驶
a千米,则11:20时距离B地还有10千米;如果改变出发时间,若每分钟行驶 a千米,则11点到达,若每分钟行驶a千米,则11:20时已经超过B地30千米.A、B两地的路程是 ________千米.
a千米,则11点到达,若每分钟行驶a千米,则11:20时已经超过B地30千米.A、B两地的路程是 ________千米.
54
分析:设AB两地距离为x千米,第一次出发时间为m,第二次出发时间为n,根据若每分钟行驶a千米,则11点到达,若每分钟行驶 a千米,则11:20时距离B地还有10千米;如果改变出发时间,若每分钟行驶
a千米,则11:20时距离B地还有10千米;如果改变出发时间,若每分钟行驶 a千米,则11点到达,若每分钟行驶a千米,则11:20时已经超过B地30千米,即可列出四个方程,从而求解.
a千米,则11点到达,若每分钟行驶a千米,则11:20时已经超过B地30千米,即可列出四个方程,从而求解.
解答:设AB两地距离为x千米,第一次出发时间为m,第二次出发时间为n,根据题意得
x=(11-m)a,①
x-10= (11+
(11+ -m) ②
-m) ②
x=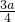 (11-n) ③
(11-n) ③
x+30=a(11+ -n) ④
-n) ④
由①②得 =
= -
-
由③④得 =
= -
-
∴ -
- =
= -
-
即 -x=(x+30)-
-x=(x+30)-
解得x=54
点评:本题主要考查了分式方程的应用,正确设未知数,找出题目中的相等关系是解题的关键.在解题时可以设出一些未知数,而在解题的过程中可以不用求解.
分析:设AB两地距离为x千米,第一次出发时间为m,第二次出发时间为n,根据若每分钟行驶a千米,则11点到达,若每分钟行驶
 a千米,则11:20时距离B地还有10千米;如果改变出发时间,若每分钟行驶
a千米,则11:20时距离B地还有10千米;如果改变出发时间,若每分钟行驶 a千米,则11点到达,若每分钟行驶a千米,则11:20时已经超过B地30千米,即可列出四个方程,从而求解.
a千米,则11点到达,若每分钟行驶a千米,则11:20时已经超过B地30千米,即可列出四个方程,从而求解.解答:设AB两地距离为x千米,第一次出发时间为m,第二次出发时间为n,根据题意得
x=(11-m)a,①
x-10=
 (11+
(11+ -m) ②
-m) ②x=
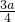 (11-n) ③
(11-n) ③x+30=a(11+
 -n) ④
-n) ④由①②得
 =
= -
-
由③④得
 =
= -
-
∴
 -
- =
= -
-
即
 -x=(x+30)-
-x=(x+30)-
解得x=54
点评:本题主要考查了分式方程的应用,正确设未知数,找出题目中的相等关系是解题的关键.在解题时可以设出一些未知数,而在解题的过程中可以不用求解.

练习册系列答案
相关题目
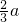 千米,则11:20时距离B地还有10千米;如果改变出发时间,若每分钟行驶
千米,则11:20时距离B地还有10千米;如果改变出发时间,若每分钟行驶 千米,则11点到达,若每分钟行驶a千米,则11:20时已超过30千米,求AB两地距离.
千米,则11点到达,若每分钟行驶a千米,则11:20时已超过30千米,求AB两地距离.