题目内容
(2012•路南区一模)如图①,在△ABC中,AB=BC,∠ABC=120°,点P是线段AC上的动点(点P与点A、点C不重合),连接BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连接AA1,直线AA1分别交直线PB、直线BB1于点E,F.
(1)如图①,当0°<α<60°时,在α角变化过程中,△APA1与△BPB1始终存在
(2)如图②,设∠ABP=β,当120°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图③,当α=120°时,点E、F与点B重合.已知AB=4,设AP=x,S=△A1BB1面积,求S关于x的函数关系式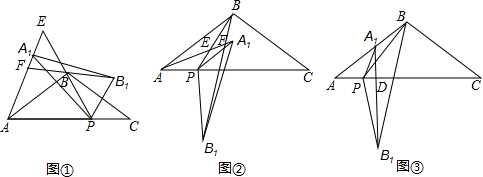
(1)如图①,当0°<α<60°时,在α角变化过程中,△APA1与△BPB1始终存在
相似
相似
关系(填“相似”或“全等”),同时可得∠A1AP=
=
∠B1BP(填“=”或“<”“>”关系).请说明△BEF与△AEP之间具有相似关系;(2)如图②,设∠ABP=β,当120°<α<180°时,在α角变化过程中,是否存在△BEF与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;
(3)如图③,当α=120°时,点E、F与点B重合.已知AB=4,设AP=x,S=△A1BB1面积,求S关于x的函数关系式

分析:(1)由旋转角相等得到一对角相等,且两对边相等,可得出三角形APA1与三角形BPB1为顶角相等的等腰三角形,利用内角和定理得到底角相等,再根据对顶角相等,等量代换得到一对角相等,又一对角为公共角,利用两对对应角相等的两三角形相似即可得到三角形BEF与三角形AEP相似;
(2)存在,理由为:由(1)得出三角形BEF与三角形AEP相似,要使两三角形全等,只需找出一对角相等,即BE=AE即可,此时利用等边对等角得到一对角相等,由AB=BC,∠ABC=120°,求出∠BAC的度数,表示出∠PAA1的度数,由∴∠BAE=∠ABP=∠BAC-∠PAA1,将各自的值代入即可列出两三角形全等时,α与β满足的关系;
(3)过点P做PH⊥AA1于点H,过点B做BM⊥B1A1交B1A1的延长线于点M,如图③所示,由旋转的性质得到△APB≌△A1PB1,根据全等三角形的对应边相等,对应角相等得到∠BAP=∠B1A1P,AB=A1B1=4,由∠APA1=α=120°,利用三角形的内角和定理得到∠BAP=∠PA1A=∠B1A1P=30°,进而得到∠AA1D=∠BA1M=60°,在Rt△PHA和Rt△BM A1中,利用锐角三角函数定义由x表示出AH,AA1,表示出A1B,利用锐角三角形函数定义表示出BM,三角形A1BB1为B1A1为底边,BM为高,利用三角形的面积公式即可列出S关于x的函数解析式.
(2)存在,理由为:由(1)得出三角形BEF与三角形AEP相似,要使两三角形全等,只需找出一对角相等,即BE=AE即可,此时利用等边对等角得到一对角相等,由AB=BC,∠ABC=120°,求出∠BAC的度数,表示出∠PAA1的度数,由∴∠BAE=∠ABP=∠BAC-∠PAA1,将各自的值代入即可列出两三角形全等时,α与β满足的关系;
(3)过点P做PH⊥AA1于点H,过点B做BM⊥B1A1交B1A1的延长线于点M,如图③所示,由旋转的性质得到△APB≌△A1PB1,根据全等三角形的对应边相等,对应角相等得到∠BAP=∠B1A1P,AB=A1B1=4,由∠APA1=α=120°,利用三角形的内角和定理得到∠BAP=∠PA1A=∠B1A1P=30°,进而得到∠AA1D=∠BA1M=60°,在Rt△PHA和Rt△BM A1中,利用锐角三角函数定义由x表示出AH,AA1,表示出A1B,利用锐角三角形函数定义表示出BM,三角形A1BB1为B1A1为底边,BM为高,利用三角形的面积公式即可列出S关于x的函数解析式.
解答:解:(1)∵∠APA1=∠BPB1=α,AP=A1P,BP=B1P,
∴∠PAA1=∠PBB1=
(180°-α)=90°-
,
∵∠PBB1=∠EBF,
∴∠EBF=∠PAE,又∠BEF=∠AEP,
∴△BEF∽△AEP;
故答案为:相似,=;
(2)存在,同上可证△BEF∽△AEP,
∴若要使得△BEF≌△AEP,只需满足BE=AE即可,
∴∠BAE=∠ABE,
∵∠ABC=120°,AB=BC,∠APA1=α,AP=A1P,
∴∠BAC=30°,∠PAA1=90°-
,
∴∠BAE=∠ABP=∠BAC-∠PAA1,
∴β=30°-(90°-
)=
-60°,
则当△BEF≌△AEP时,β=
-60°(或α=2β+120°);
(3)过点P做PH⊥AA1于点H,
过点B做BM⊥B1A1交B1A1的延长线于点M,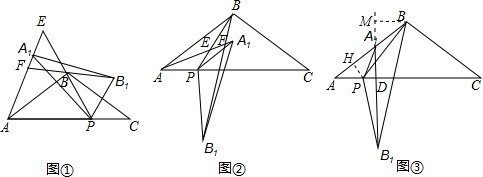
∵△APB≌△A1PB1,
∴∠BAP=∠B1A1P,AB=A1B1=4,
∵∠APA1=α=120°,
∴∠BAP=∠PA1A=∠B1A1P=30°,
∴∠AA1D=∠BA1M=60°,
∴在Rt△PHA和Rt△BM A1中,AP=x,AH=
x,AA1=
x,
∴A1B=AB-AA1=4-
x,
∴BM=A1Bsin60°=
(4-
x)=2
-
x,
则S=
A1B1•BM=
×4×(2
-
x)=4
-3x.
∴∠PAA1=∠PBB1=
| 1 |
| 2 |
| α |
| 2 |
∵∠PBB1=∠EBF,
∴∠EBF=∠PAE,又∠BEF=∠AEP,
∴△BEF∽△AEP;
故答案为:相似,=;
(2)存在,同上可证△BEF∽△AEP,
∴若要使得△BEF≌△AEP,只需满足BE=AE即可,
∴∠BAE=∠ABE,
∵∠ABC=120°,AB=BC,∠APA1=α,AP=A1P,
∴∠BAC=30°,∠PAA1=90°-
| α |
| 2 |
∴∠BAE=∠ABP=∠BAC-∠PAA1,
∴β=30°-(90°-
| α |
| 2 |
| α |
| 2 |
则当△BEF≌△AEP时,β=
| α |
| 2 |
(3)过点P做PH⊥AA1于点H,
过点B做BM⊥B1A1交B1A1的延长线于点M,

∵△APB≌△A1PB1,
∴∠BAP=∠B1A1P,AB=A1B1=4,
∵∠APA1=α=120°,
∴∠BAP=∠PA1A=∠B1A1P=30°,
∴∠AA1D=∠BA1M=60°,
∴在Rt△PHA和Rt△BM A1中,AP=x,AH=
| ||
| 2 |
| 3 |
∴A1B=AB-AA1=4-
| 3 |
∴BM=A1Bsin60°=
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
则S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
点评:此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,锐角三角函数定义,等腰三角形的性质,三角形的内角和定理,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
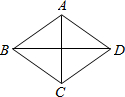 (2012•路南区一模)如图,在菱形ABCD中,两条对角线AC=12,BD=16,则此菱形的边长为( )
(2012•路南区一模)如图,在菱形ABCD中,两条对角线AC=12,BD=16,则此菱形的边长为( )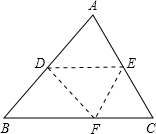 (2012•路南区一模)如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中一定正确的是( )
(2012•路南区一模)如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中一定正确的是( )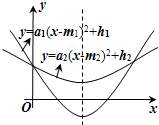 (2012•路南区一模)如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系中不正确的是( )
(2012•路南区一模)如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系中不正确的是( ) (2012•路南区一模)如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm2、100cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,设甲容器的容积为x cm3,则根据题意得( )
(2012•路南区一模)如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm2、100cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,设甲容器的容积为x cm3,则根据题意得( )