题目内容
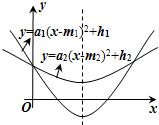 (2012•路南区一模)如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系中不正确的是( )
(2012•路南区一模)如图,直角坐标系中,两条抛物线有相同的对称轴,下列关系中不正确的是( )分析:根据函数的图象和抛物线的对称轴所在的位置判断出m2,h2,m1,h1的正负,再根据实数比较大小的法则进行比较即可.
解答:解:①由函数y=a2(x-m2)2+h2可知,m2>0,h2>0,
由函数y=a1(x-m1)2+h1可知,m1>0,h1<0,
∵两抛物线有相同的对称轴,
∴m1=m2,故B正确;
②∵h2>0,h1<0,
∴h2>h1,故C正确;
③由图象可知:m1>0,m2>0,
故D正确;
④由图象可知:a1>a2,故A不正确;
故选A.
由函数y=a1(x-m1)2+h1可知,m1>0,h1<0,
∵两抛物线有相同的对称轴,
∴m1=m2,故B正确;
②∵h2>0,h1<0,
∴h2>h1,故C正确;
③由图象可知:m1>0,m2>0,
故D正确;
④由图象可知:a1>a2,故A不正确;
故选A.
点评:此题考查了二次函数图象与系数的关系,解题的关键是根据函数的图象求出二次函数的系数,运用顶点坐标及对称轴判断横坐标及纵坐标的大小.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
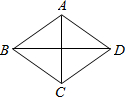 (2012•路南区一模)如图,在菱形ABCD中,两条对角线AC=12,BD=16,则此菱形的边长为( )
(2012•路南区一模)如图,在菱形ABCD中,两条对角线AC=12,BD=16,则此菱形的边长为( ) (2012•路南区一模)如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中一定正确的是( )
(2012•路南区一模)如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,下列结论中一定正确的是( ) (2012•路南区一模)如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm2、100cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,设甲容器的容积为x cm3,则根据题意得( )
(2012•路南区一模)如图,在水平桌面上有甲、乙两个内部呈圆柱形的容器,内部底面积分别为80cm2、100cm2,且甲容器装满水,乙容器是空的.若将甲中的水全部倒入乙中,则乙中的水位高度比原先甲的水位高度低了8cm,设甲容器的容积为x cm3,则根据题意得( )