题目内容
一辆汽车以每小时80km的速度从甲地开往320km外的乙地.
(1)写出汽车离甲地的距离s1与时间t的函数关系式.并画出函数图象;
(2)写出汽车离乙地的距离s2与时间t的函数关系式.并画出函数图象.
(1)写出汽车离甲地的距离s1与时间t的函数关系式.并画出函数图象;
(2)写出汽车离乙地的距离s2与时间t的函数关系式.并画出函数图象.
分析:(1)根据距离=速度×时间得到关系式,由关系式来画出图象;
(2)根据汽车离乙地的距离=总距离-汽车离甲地的距离列出关系式,然后由“两点确定一条直线”作出图象.
(2)根据汽车离乙地的距离=总距离-汽车离甲地的距离列出关系式,然后由“两点确定一条直线”作出图象.
解答: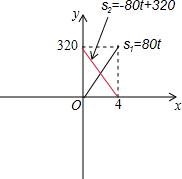 解:(1)依题意,得
解:(1)依题意,得
s1=80t(0≤t≤4),
所以,汽车离甲地的距离s1与时间t为一次函数,其图象是过原点的一条直线.
所以当t=4时,s1=320,故该直线经过点(0,0)和(1,80).
其图象如图所示;
(2)依题意,得
s2=320-80t,即s2=-80t+320(0≤t≤4),
所以,汽车离甲地的距离s2与时间t为一次函数,其图象是一条直线.
所以当t=0时,s2=320;当s2=0时,t=4,
故该直线经过点(0,320)和(4,0).
其图象如图所示.
 解:(1)依题意,得
解:(1)依题意,得s1=80t(0≤t≤4),
所以,汽车离甲地的距离s1与时间t为一次函数,其图象是过原点的一条直线.
所以当t=4时,s1=320,故该直线经过点(0,0)和(1,80).
其图象如图所示;
(2)依题意,得
s2=320-80t,即s2=-80t+320(0≤t≤4),
所以,汽车离甲地的距离s2与时间t为一次函数,其图象是一条直线.
所以当t=0时,s2=320;当s2=0时,t=4,
故该直线经过点(0,320)和(4,0).
其图象如图所示.
点评:本题考查了一次函数的应用.画图象时,注意定义域的取值范围.

练习册系列答案
相关题目
某段隧道全长9公里,有一辆汽车以每小时60公里到80公里之间的速率通过该隧道.下列何者可能是该车通过隧道所用的时间( )
| A、6分钟 | B、8分钟 | C、10分钟 | D、12分钟 |