题目内容
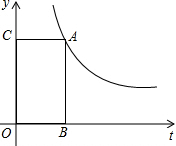 (2012•六盘水)如图为反比例函数y=
(2012•六盘水)如图为反比例函数y=| 1 |
| x |
分析:首先表示出矩形边长,再利用长与宽的积为定值,且为正数,故考虑利用基本不等式即可解决.
解答:解:∵反比例函数y=
在第一象限的图象,点A为此图象上的一动点,过点A分别作
AB⊥x轴和AC⊥y轴,垂足分别为B,C.
∴四边形OBAC为矩形,
设宽BO=x,则AB=
,周长的一半表示为s,
则s=x+
≥2
=2,
当且仅当x=
,即x=1时,取等号.
故函数s=x+
(x>0)的最小值为2.
故2(x+
)=2×2=4,
则四边形OBAC周长的最小值为4.
故选:A.
| 1 |
| x |
AB⊥x轴和AC⊥y轴,垂足分别为B,C.
∴四边形OBAC为矩形,
设宽BO=x,则AB=
| 1 |
| x |
则s=x+
| 1 |
| x |
x•
|
当且仅当x=
| 1 |
| x |
故函数s=x+
| 1 |
| x |
故2(x+
| 1 |
| x |
则四边形OBAC周长的最小值为4.
故选:A.
点评:此题考查了反比例函数的综合应用以及函数的最值问题,解答本题的关键是掌握不等式的基本性质,即a+b≥2
,难度一般.
| ab |

练习册系列答案
相关题目
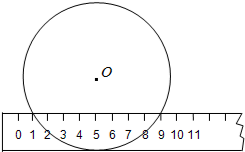 (2012•六盘水)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为
(2012•六盘水)当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为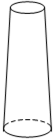 (2012•六盘水)如图是教师每天在黑板上书写用的粉笔,它的主视图是( )
(2012•六盘水)如图是教师每天在黑板上书写用的粉笔,它的主视图是( )