题目内容
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与x轴交于点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)求证:∠DAB=∠ACB;
(3)点Q在抛物线上,且△ADQ是以AD为底的等腰三角形,求Q点的坐标.

【答案】(1)(﹣1,4);(2)∠DAB=∠ACB;(3)![]() ,
,![]()
【解析】试题分析:(1)把B、C坐标代入抛物线解析式中,解方程组即可得到抛物线解析式,从而得到抛物线顶点坐标;
(2)由tan∠OCB=![]() .tan∠DAC=
.tan∠DAC=![]() ,得到∠DAC=∠OCB,从而得到结论;
,得到∠DAC=∠OCB,从而得到结论;
(3)令Q(x,y)且满足![]() ,由△ADQ是以AD为底的等腰三角形,得到QD2=QA2,从而得到x-2+2y=0.解方程组
,由△ADQ是以AD为底的等腰三角形,得到QD2=QA2,从而得到x-2+2y=0.解方程组![]() ,即可得到结论.
,即可得到结论.
试题解析:解:(1)把B(1,0)和C(0,3)代入![]() 中,
中,
得:![]() ,解得:
,解得:![]() .
.
∴抛物线的解析式是:![]() ,∴顶点坐标D(-1,4).
,∴顶点坐标D(-1,4).
(2)令y=0,则![]() ,x1=-3,x2=1,∴A(-3,0),∴OA=OC=3,∴∠CAO=∠OCA.在Rt△BOC中,tan∠OCB=
,x1=-3,x2=1,∴A(-3,0),∴OA=OC=3,∴∠CAO=∠OCA.在Rt△BOC中,tan∠OCB=![]() .
.
∵AC=![]() ,DC=
,DC=![]() ,AD=
,AD=![]() ,∴AC2+DC2=20,AD2=20,∴AC2+DC2=AD2,∴△ACD是直角三角形且∠ACD=90°,∴tan∠DAC=
,∴AC2+DC2=20,AD2=20,∴AC2+DC2=AD2,∴△ACD是直角三角形且∠ACD=90°,∴tan∠DAC=![]() .
.
又∵∠DAC和∠OCB都是锐角,∴∠DAC=∠OCB,∴∠DAC+∠CAO=∠BCO+∠OCA,即∠DAB=∠ACB.
(3)令Q(x,y)且满足![]() ,A(-3,0),D(-1,4).∵△ADQ是以AD为底的等腰三角形,∴QD2=QA2,即
,A(-3,0),D(-1,4).∵△ADQ是以AD为底的等腰三角形,∴QD2=QA2,即![]() ,化简得:x-2+2y=0.
,化简得:x-2+2y=0.
由![]() ,解得:
,解得: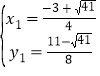 ,
, ,
,
∴点Q的坐标是(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).

【题目】某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司一共62辆![]() 两种型号客车作为交通工具.
两种型号客车作为交通工具.
下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人/辆 | 380元/辆 |
| 20人/辆 | 280元/辆 |
注:载客量指的是每辆客车最多可载该校师生的人数.设学校租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
(1)求![]() 与
与![]() 的函数解析式,请直接写出
的函数解析式,请直接写出![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案总费用最省?最省的总费用是多少?



