题目内容
【题目】如图所示,在Rt△ABC和Rt△ADE中,AB=AC, AD=AE,CE与BD相交于点M,BD与AC交于点N,试猜想BD与CE有何关系?说明理由。

【答案】BD=CE且BD⊥CE,证明见解析.
【解析】试题分析:结论:BD=CE且BD⊥CE.只要证明△BAD≌△CAE,再利用“8字型”证直角.
试题解析:结论:BD=CE且BD⊥CE.
理由:∵△ABC和△ADE是直角三角形,
∴∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△BAD与△CAE中,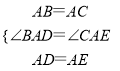 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,∠ABD=∠ACE,
∵∠ABD+∠ANB+∠BAC=180°,
∠ACE+∠CNM+∠NMC=180°,
∠ANB=∠CNM,
∴∠NMC=∠BAC=90°,
∴BD⊥CE,
即BD=CE且BD⊥CE.

练习册系列答案
相关题目
【题目】某班6名同学的身高(单位:cm)情况如下表:
同学 | A | B | C | D | E | F |
身高 | 165 | 166 | 171 | |||
身高与班级平均身高的差值 | -1 | +2 | -3 | +3 |
(1)完成表中空白的部分;
(2)他们的最高身高与最矮身高相差多少?
(3)他们6人的平均身高是多少?
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭,小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如下表),以50 km为标准,多于50 km的记为“+”,不足50 km的记为“-”,刚好50 km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | -8 | -11 | -14 | 0 | -16 | +41 | +8 |
(1)请求出这七天中平均每天行驶多少千米?
(2)若每天行驶100 km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?



