题目内容

菱形ABCD的周长为20cm，∠ABC=120°，则对角线BD等于（　　）
A、4cmB、6cmC、5cmD、10cm
练习册系列答案
相关题目
如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：
①∠BOC=90°+
1
2
∠A；
②以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切；
③EF是△ABC的中位线；
④设OD=m，AE+AF=n，则S△AEF=
1
2
mn．
其中正确的结论是（　　）
A、①②③B、①③④
C、②③④D、①②④
四边形ABCD中，AC、BD相交于点O，不能判定它是平行四边形的条件是（　　）
A、AB∥CD，AD∥BCB、AO=CO，BO=DOC、AB∥CD，AD=BCD、AB=CD，AD=BC
菱形的两条对角线长分别是6和8，则此菱形的边长是（　　）
A、10B、8C、6D、5
如图，菱形ABCD的对角线AC，BD相交于点O，AC=8，BD=6，以AB为直径作一个半圆，则图中阴影部分的面积为（　　）
A、25π-6
B、
25
2
π-6
C、
25
6
π-6
D、
25
8
π-6
一个菱形被一条直线分成面积为x，y的两部分，则y与x之间的函数图象只可能是（　　）
A、B、C、D、
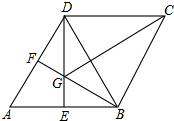如图，在菱形ABCD中，∠A=60°，E，F分别是AB，AD的中点，DE，BF相交于点G，连接BD，CG，有下列结论：
①∠BGD=120°；②BG+DG=CG；③△BDF≌△CGB．
其中正确的结论有（　　）
A、0个B、1个C、2个D、3个
下列说法中正确的是（　　）
A、对角线互相垂直的四边形是菱形B、有一个角是60°的等腰三角形是等边三角形C、有一组对边相等的四边形是平行四边形D、等腰梯形的对角线互相平分
已知四边形ABCD是平行四边形，对角线AC与BD相交于点O，下列结论中不正确的是（　　）
A、当AB=BC时，四边形ABCD是菱形B、当AC⊥BD时，四边形ABCD是菱形C、当OA=OB时，四边形ABCD是矩形D、当∠ABD=∠CBD时，四边形ABCD是矩形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网