题目内容
【题目】已知,如图,在Rt△ABC中,∠ACB=900,AD平分∠CAB交BC于点D,过点C作CE⊥AD,垂足为E,CE的延长线交AB于点F,过点E作EG∥BC交AB于点G, ![]() ,
, ![]() ,求:(1)AC的长(2)EG的长.
,求:(1)AC的长(2)EG的长.

【答案】(1)4;(2)4
【解析】试题分析:(1)∠CAD是公共角,∠ACB=∠AEC=90°,所以△ACE和△ADC相似,根据相似三角形对应边成比例,列出比例式整理即可得到AC2=AEAD,代入数据计算即可;
(2)根据勾股定理求出BC的长度为8,再根据AD平分∠CAB交BC于点D,CE⊥AD证明△ACE和△AFE全等,根据全等三角形对应边相等,CE=EF,最后根据三角形的中位线平行于第三边并且等于第三边的一半EG=![]() BC.
BC.
解:∵CE⊥AD,
∴∠AEC=90°,
∵∠ACB=90°,
∴∠AEC=∠ACB,
又∠CAE=∠CAE,
∴△ACE∽△ADC,
∴AC:AE=AD:AC,
即AC2=AEAD,
∵AEAD=16,
∴AC2=16,
∴AC=4;
(2)在△ABC中,
BC=![]() =
= ![]() ,
,
∵AD平分∠CAB交BC于点D,
∴∠CAE=∠FAE,
∵CE⊥AD,
∴∠AEC=∠AEF=90°,
在△ACE和△AFE中,
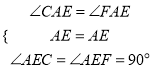 ,
,
∴△ACE≌△AFE(ASA),
∴CE=EF,
∵EG∥BC,
∴EG=![]() BC=
BC=![]() ×8=4.
×8=4.

练习册系列答案
相关题目


