题目内容
【题目】已知![]() 和
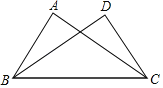
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
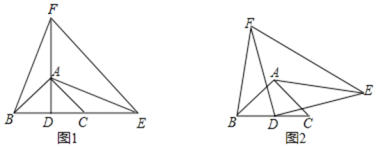
(1)当点![]() ,
,![]() 分别在
分别在![]() 和
和![]() 上时,如图1,试猜想线段
上时,如图1,试猜想线段![]() 和
和![]() 的数量关系,请直接写出你得到的结论(不要求证明);
的数量关系,请直接写出你得到的结论(不要求证明);
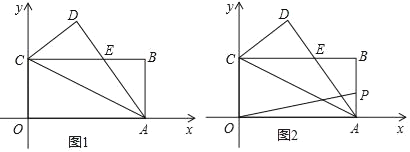
(2)将![]() 绕点
绕点![]() 逆时针方向旋转一定角度后(旋转角度大于
逆时针方向旋转一定角度后(旋转角度大于![]() ,小于或等于
,小于或等于![]() ),如图2,请问:(1)中的结论是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
),如图2,请问:(1)中的结论是否仍然成立?如果成立,请给予证明;如果不成立,请说明理由.
【答案】(1)AE=BF;(2)(1)中的结论仍然成立,证明见解析
【解析】
(1)根据等腰直角三角形的性质,通过证明三角形全等即可得结论;
(2)根据旋转的性质得角相等,然后证明三角形全等即可得结论.
解:(1)AE=BF.
∵△ABC和△DEF是等腰三角形,D是BC的中点,
∴AD=BD=DC,AD⊥BC,
∴∠ADC=∠ADB=90°,DE=DF,
在△BDF与△ADE中,
 ,
,
∴△BDF≌△ADE(SAS)
∴AE=BF.
(2)(1)中的结论仍然成立.理由如下:
如图:连接AD,
∵△ABC和△DEF是等腰三角形,D是BC的中点,
∴AD=BD=DC,AD⊥BC,
∴∠ADC=∠ADB=90°,DE=DF,
根据旋转的性质,可知
∠CDE=∠ADF,
又∠BDF=90°∠ADF,∠ADE=90°∠CDE,
∴∠BDF=∠ADE
∴△BDF≌△ADE(SAS)
∴BF=AE.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目