题目内容
【题目】如图，抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标（1，n）与y轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：①3a+b＜0；②﹣1≤a≤﹣
；③对于任意实数m，a+b≥am2+bm总成立；④关于x的方程ax2+bx+c＝n﹣1有两个不相等的实数根．其中结论正确的个数为（ ）
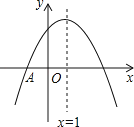
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
利用抛物线开口方向得到a＜0，再由抛物线的对称轴方程得到b＝﹣2a，则3a+b＝a，于是可对①进行判断；利用2≤c≤3和c＝﹣3a可对②进行判断；利用二次函数的性质可对③进行判断；根据抛物线y＝ax2+bx+c与直线y＝n﹣1有两个交点可对④进行判断．
解：∵抛物线开口向下，
∴a＜0，
而抛物线的对称轴为直线x＝﹣
＝1，即b＝﹣2a，
∴3a+b＝3a﹣2a＝a＜0，所以①正确；
∵2≤c≤3，
而c＝﹣3a，
∴2≤﹣3a≤3，
∴﹣1≤a≤﹣
，所以②正确；
∵抛物线的顶点坐标（1，n），
∴x＝1时，二次函数值有最大值n，
∴a+b+c≥am2+bm+c，
即a+b≥am2+bm，所以③正确；
∵抛物线的顶点坐标（1，n），
∴抛物线y＝ax2+bx+c与直线y＝n﹣1有两个交点，
∴关于x的方程ax2+bx+c＝n﹣1有两个不相等的实数根，所以④正确．
故选：D．
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案【题目】随着移动终端设备的升级换代，手机已经成为我们生活中不可缺少的一部分，为了解中学生在假期使用手机的情况(选项：A．和同学亲友聊天；B．学习；C．购物；D．玩游戏；E．其它)，端午节后某中学在全校范围内随机抽取了若干名学生进行调査，得到如图表(部分信息未给出)：
选项 | 频数 | 百分比 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
根据以上信息解答下列问题：
(1)这次被调查的学生有多少人？
(2)求表中m，n，p的值，并补全条形统计图；
(3)若该中学约有2400名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？并根据以上调査结果，就中学生如何合理使用手机给出你的一条建议．
