Question

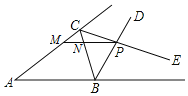
【题目】如图，在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD，其中AM=AN.

(1)求证：Rt△ABM≌Rt△AND

(2)线段MN与线段AD相交于T，若AT=,求的值

Answer 1

【答案】（1）证明见解析；（2）.

【解析】（1）利用HL证明即可；

（2）证明△DNT∽△AMT，可得，由AT=AD，推出，在Rt△ABM中，tan∠ABM=．

（1）∵AD=AB，AM=AN，∠AMB=∠AND=90°

∴Rt△ABM≌Rt△AND（HL）．

（2）由Rt△ABM≌Rt△AND易得：∠DAN=∠BAM，DN=BM

∵∠BAM+∠DAM=90°；∠DAN+∠ADN=90°

∴∠DAM=∠AND

∴ND∥AM

∴△DNT∽△AMT

∴

∵AT=AD，

∴

∵Rt△ABM

∴tan∠ABM=．