题目内容
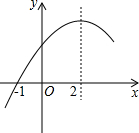 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:
二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(-1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>-1时,y的值随x值的增大而增大.
其中正确的结论有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
练习册系列答案
相关题目
已知抛物线y=x2-ax+a+3对称轴在y轴的右侧,顶点在x轴上,则a的值是( )
| A、6 | B、-2 | C、6或-2 | D、4 |
已知抛物线y=ax2+bx+c(a≠0)经过点(1,1)和(-1,0).下列结论:
①a-b+c=0;
②b2>4ac;
③当a<0时,抛物线与x轴必有一个交点在点(1,0)的右侧;
④抛物线的对称轴为x=-
.
其中结论正确的个数有( )
①a-b+c=0;
②b2>4ac;
③当a<0时,抛物线与x轴必有一个交点在点(1,0)的右侧;
④抛物线的对称轴为x=-
| 1 |
| 4a |
其中结论正确的个数有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
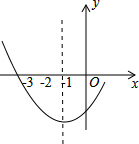 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④3a+c=0;其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④3a+c=0;其中说法正确的是( )| A、①② | B、②③ | C、①②④ | D、②③④ |
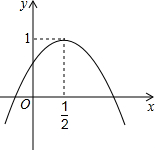 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为(| 1 |
| 2 |
| A、4 | B、3 | C、2 | D、1 |
将抛物线y=5x2向右平移2个单位.再向上平移3个单位.得到的抛物线是( )
| A、y=5(x+2)2+3 | B、y=5(x+2)3-3 | C、y=5(x-2)2+3 | D、y=5(x-2)2-3 |

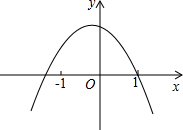 已知函数y=-(x-m)(x-n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=
已知函数y=-(x-m)(x-n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=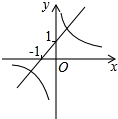
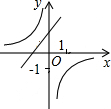
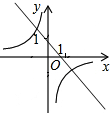
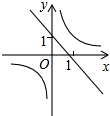
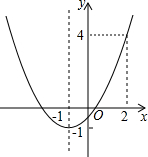 已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列结论: