题目内容
著名的斐波那契数列指的是数列:1,1,2,3,5,8,13,21,34,…,这个数列从第三项开始,每一项都等于前两项之和.该数列有很多性质,“相邻两个斐波那契数的比值随序号的增加而逐渐趋于黄金分割比 =0.6180339887…”是其中的一个性质.请经过探究,猜测该数列中的第2010项与2011项的比值与黄金分割比的大小关系为
=0.6180339887…”是其中的一个性质.请经过探究,猜测该数列中的第2010项与2011项的比值与黄金分割比的大小关系为
- A.大于
- B.等于
- C.小于
- D.无法确定
C
分析:根据斐波那契数列中奇数项与后一项的比值大于黄金分割比,偶数项与后一项的比值小于黄金分割比即可求解.
解答:∵第2010项是偶数项,
∴第2010项与2011项的比值小于黄金分割比.
故选C.
点评:本题结合斐波那契数列考查了黄金分割,斐波那契数列这个值是1最小,也就是前后项之比接近黄金分割最快,我们称为黄金特征,黄金特征1的数列只有斐波那契数列,是独生数列.
分析:根据斐波那契数列中奇数项与后一项的比值大于黄金分割比,偶数项与后一项的比值小于黄金分割比即可求解.
解答:∵第2010项是偶数项,
∴第2010项与2011项的比值小于黄金分割比.
故选C.
点评:本题结合斐波那契数列考查了黄金分割,斐波那契数列这个值是1最小,也就是前后项之比接近黄金分割最快,我们称为黄金特征,黄金特征1的数列只有斐波那契数列,是独生数列.

练习册系列答案
相关题目
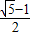 =0.6180339887…”是其中的一个性质.请经过探究,猜测该数列中的第2010项与2011项的比值与黄金分割比的大小关系为( )
=0.6180339887…”是其中的一个性质.请经过探究,猜测该数列中的第2010项与2011项的比值与黄金分割比的大小关系为( )