题目内容
(2012•常州)在平面直角坐标系xOy中,已知点P(3,0),⊙P是以点P为圆心,2为半径的圆,若一次函数y=kx+b的图象过点A(-1,0)且与⊙P相切,则k+b的值为
±
2
| ||
| 3 |
±
.2
| ||
| 3 |
分析:根据题意画出相应的图形,如图所示当直线AB与圆P相切,切点为B点且B在第一象限时,连接PB,由AB为圆P的切线,利用切线的性质得到AB垂直于BP,可得出三角形ABP为直角三角形,由A和P的坐标求出OA与OP的长,用OA+OP求出AP的长,可得出BP等于AP的一半,根据直角三角形中一直角边等于斜边的一半,可得出此直角边所对的角为30°,得到∠BAP为30°,在直角三角形AOC中,由C的坐标求出OC的长,利用锐角三角函数定义表示出tan30°,将OA的值并利用特殊角的三角函数值化简,求出OC的长,确定出C的坐标,设直线AC的解析式为y=kx+b,将A和C的坐标代入得到关于k与b的二元一次方程组,求出方程组的解得到k与b的值,进而求出k+b的值;当直线AB与圆P相切,B为切点,且B在第二象限时,同理求出k+b的值,综上,得到满足题意k+b的值.
解答:解:根据题意画出相应的图形,如图所示:
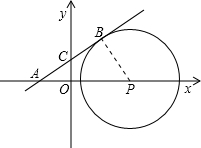
当直线AB与圆P相切,设切点为B点,且切点B在第一象限时,
连接PB,由AB为圆P的切线,得到BP⊥AB,
又∵A(-1,0),P(3,0),
∴OA=1,OP=3,又BP=2,
则AP=OA+OP=1+3=4,
在Rt△ABP中,BP=
AP,
可得出∠BAP=30°,
在Rt△ACO中,OA=1,∠BAP=30°,
∴tan∠BAP=tan30°=
=OC,
∴OC=
,即C(0,
),
设直线AC的解析式为y=kx+b,将A和C的坐标代入得:
,
解得:
,
∴k+b=
;
当直线AB与圆P相切时,切点B在第四象限时,同理得到k=b=-
,
可得k+b=-
,
综上,k+b=±
.
故答案为:±
.

当直线AB与圆P相切,设切点为B点,且切点B在第一象限时,
连接PB,由AB为圆P的切线,得到BP⊥AB,
又∵A(-1,0),P(3,0),
∴OA=1,OP=3,又BP=2,
则AP=OA+OP=1+3=4,
在Rt△ABP中,BP=
| 1 |
| 2 |
可得出∠BAP=30°,
在Rt△ACO中,OA=1,∠BAP=30°,
∴tan∠BAP=tan30°=
| OC |
| OA |
∴OC=
| ||
| 3 |
| ||
| 3 |
设直线AC的解析式为y=kx+b,将A和C的坐标代入得:
|
解得:
|
∴k+b=
2
| ||
| 3 |
当直线AB与圆P相切时,切点B在第四象限时,同理得到k=b=-
| ||
| 3 |
可得k+b=-
2
| ||
| 3 |
综上,k+b=±
2
| ||
| 3 |
故答案为:±
2
| ||
| 3 |
点评:此题考查了切线的性质,含30°直角三角形的判定与性质,利用待定系数法求一次函数解析式,锐角三角函数定义,以及坐标与图形性质,利用了数形结合及分类讨论的思想,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
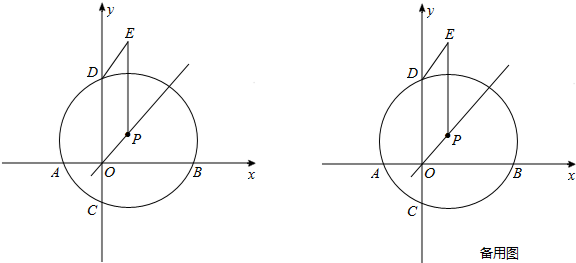
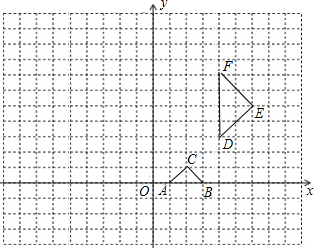 EF拼接成一个平行四边形(非正方形),写出符合要求的变换过程.
EF拼接成一个平行四边形(非正方形),写出符合要求的变换过程.