题目内容
【题目】如图,直线AB与CD相交于点O,∠BOE=∠DOF=90°.
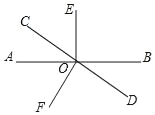
(1)写出图中与∠COE互补的所有的角(不用说明理由).
(2)问:∠COE与∠AOF相等吗?请说明理由;
(3)如果∠AOC=![]() ∠EOF,求∠AOC的度数.
∠EOF,求∠AOC的度数.
【答案】(1) ∠DOE,∠BOF;(2) 相等;(3) ∠AOC=30°.
【解析】试题分析:
(1)由题意易得∠COE+∠DOE=180°,由∠BOE=∠DOF=90°可得∠DOE=∠BOF,从而可得∠COE的补角是∠DOE和∠BOF;
(2)由∠BOE=∠DOF=90°易得∠AOE=∠COF=90°,从而可得∠COE=∠AOF;
(3)设∠AOC=x,则可得∠EOF=5x,结合∠COE=∠AOF可得∠COE=2x,由∠AOC+∠COE=∠AOE=90°列出关于x的方程,解方程求得x的值即可.
试题解析;
(1)∵直线AB与CD相交于点O,
∴∠COE+∠DOE=180°,即∠DOE是∠COE的补角,
∵∠BOE=∠DOF=90°,
∴∠BOE+∠BOD=∠DOF+∠BOD,
即:∠DOE=∠BOF,
∴与∠COE互补的角有:∠DOE,∠BOF;
(2)∠COE与∠AOF相等,
理由:∵直线AB、CD相交于点O,
∴∠AOE+∠BOE=180°,∠COF+∠DOF=180°,
又∵∠BOE=∠DOF=90°,
∴∠AOE=∠COF=90°,
∴∠AOE﹣∠AOC=∠COF﹣∠AOC,
∴∠COE=∠AOF;
(3)设∠AOC=x,则∠EOF=5x,
∴∠COE+∠AOF=∠EOF-∠AOC=5x-x=4x,
∵∠COE=∠AOF,
∴∠COE=∠AOF=2x,
∵∠AOE=90°,
∴x+2x=90°,
∴x=30°,
∴∠AOC=30°.

【题目】某校篮球队进行篮球投篮训练,下表是某队员投篮的统计结果:
投篮次数 次 | 10 | 50 | 100 | 150 | 200 |
命中次数 次 | 9 | 40 | 75 | 108 | 144 |
命中率 | 0.9 | 0.8 | 0.75 | 0.72 | 0.72 |
根据上表,你估计该队员一次投篮命中的概率大约是( )
A.0.72B.0.75C.0.8D.0.9