Question

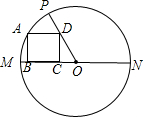
如图，以正方形ABCD的边AD、BC、CD为直径画半圆，阴影部分的面积记为m，空白部分的面积记为n，则m与n的关系为______．

Answer 1

设正方形ABCD的边长为a，
则阴影AEB的面积=（S_□ABCD-S_半圆AED-S_半圆BEC）÷2=[a²-2×

1

2

×（

a

2

）²π]÷2=

a2

2

-

πa2

8

，
S_阴影=m=S_半圆CDE+S_阴影AEB=

1

2

×

πa2

4

+

a2

2

-

πa2

8

=

a2

2

，
故n=a²-m=a²-

a2

2

=

a2

2

．
故答案为：m=n．