题目内容
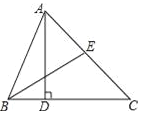
【题目】如图，AD为△ABC的高，BE为△ABC的角平分线，若∠EBA＝32°，∠AEB＝70°.
（1）求∠CAD的度数；
（2）若点F为线段BC上任意一点，当△EFC为直角三角形时，则∠BEF的度数为
【答案】（1）52°；（2）58°或20°
【解析】
（1）根据角平分线的定义、三角形内角和定理计算即可；
（2）分∠EFC=90°和∠FEC=90°两种情况解答即可．
解：（1）∵BE为△ABC的角平分线，
∴∠CBE=∠EBA=32°，
∵∠AEB=∠CBE+∠C，
∴∠C=70°-32°=38°，
∵AD为△ABC的高，
∴∠ADC=90°，
∴∠CAD=90°-∠C=52°；
（2）当∠EFC=90°时，∠BEF=90°-∠CBE=58°，
当∠FEC=90°时，∠BEF=90°70°=20°，
故答案为：58°或20°．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某剧院的观众席的座位为扇形，且按下列分式设置：
排数（x） | 1 | 2 | 3 | 4 | … |
座位数（y） | 50 | 53 | 56 | 59 | … |
（1）按照上表所示的规律，当x每增加1时，y如何变化？
（2）写出座位数y与排数x之间的关系式；
（3）按照上表所示的规律，某一排可能有90个座位吗？说说你的理由．
