题目内容
【题目】如图,在平面直角坐标系中,A9m,0、Bm,0m0,以AB为直径的⊙M交y轴正半轴于点C,CD是⊙M的切线,交x轴正半轴于点D,过A作AECD于E,交⊙于F.
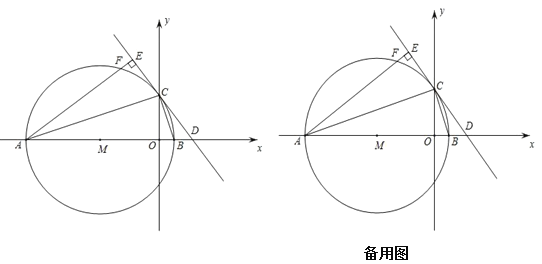
(1)求C的坐标;(用含m的式子表示)
(2)①请证明:EFOB;②用含m的式子表示AFC的周长;
(3)若![]() ,
,![]() ,
,![]() 分别表示
分别表示![]() 的面积,记
的面积,记![]() ,对于经过原点的二次函数
,对于经过原点的二次函数![]() ,当
,当![]() 时,函数y的最大值为a,求此二次函数的解析式.
时,函数y的最大值为a,求此二次函数的解析式.
【答案】(1)C(0,3m);
(2)①证明见解析;②8m+![]() ;
;
(3) ![]() 或
或![]()
【解析】
(1)连接MC,先得出MC=5m,MO=4m,再由勾股定理得出OC=3m,即可得出点C的坐标;
(2)①由弦切角定理得∠ECF=∠EAC,再证出FC=BC,再证出△CEF≌△COB,可得到EF=OB;
②由△CEF≌△COB可得AE=AO,用勾股定理求出AC、BC.再用等量代换计算可得到AFC的周长
(3)先用三角函数求出OD,再用勾股定理列出方程,得到m=1,从而求得![]() 的面积,再求出k值。再根据二次函数的性质列出方程求得a的值,从而问题得解。
的面积,再求出k值。再根据二次函数的性质列出方程求得a的值,从而问题得解。
解:(1)连接MC,

∵A9m,0、Bm,0m0,
∴AB=10m,MC=5m,MO=4m
由勾股定理得![]()
解得:OC=3m
∴C(0,3m)
(2)①证明:连接CF,

∵CE是⊙M的切线,
∴∠ECF=∠EAC,
∵AB是直径,
∴∠ACB=90°
∴∠CAB=∠BCO,
∵A,F,C,B共圆,
∴∠EFC=∠OBC,
又∵AE⊥CE
∴∠CEF=∠BOC=90°,
∴∠ECF=∠BCO,
∴∠EAC=∠CAB
∴CF=CB
在△CEF和△COB中

∴△CEF≌△COB
∴EF=BO
②∵△CEF≌△COB
∴CE=CO,
∴△ACE≌△ACO(HL)
∴AE=AO
∵![]()
![]()
AFC的周长=AF+FC+AC=AE-EF+FC+AC
=AO-BO+FC+AC
=9m-m+![]() +
+![]()
=8m+![]()
(3)∵CD是⊙M的切线,
易证∠OCD=∠OMC
∴sin∠OMC= sin∠OCD
![]()
即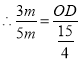
得![]()
在Rt△OCD中,
![]()
而CO=3m
∴m=1
∴AF=8,CE=3, ![]()
∴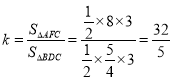
二次函数![]() 的图象过原点,则c=0
的图象过原点,则c=0
得![]()
对称轴为直线![]()
当![]() 时,即
时,即![]()
分两种情况,a<0时,由函数的性质可知,![]() 时,y=a,
时,y=a,
∴![]()
解得![]()
∴此二次函数的解析式为:![]()
A>0时,由函数的性质可知,x=4时,y=a,
∴a=16a-4
解得![]()
∴此二次函数的解析式为:![]()
综上,此二次函数的解析式为:![]() 或
或![]()
故答案为:![]() 或
或![]()

【题目】某赛季篮球甲A 联赛部分球队积分榜如下:
队名 | 比赛场次 | 胜场 | 负场 | 积分 |
八一双鹿 | 20 | 18 | 2 | 38 |
北京首钢 | 20 | 14 | 6 | 34 |
浙江万马 | 20 | 7 | 13 | 27 |
沈部雄狮 | 20 | 0 | 20 | 20 |
(1)该比赛胜1场的积分为 分,负1场的积分为 分, 列式表示积分与胜、负场数之间的数量关系,假设胜场数为m场,则这次比赛的积分是 (直接写出结果)
(2)某队的胜场总积分能等于它的负场总积分吗?
【题目】仙居吾悦广场于![]() 年
年![]() 月
月![]() 日开业,商场内两家服装店举行开业大酬宾活动,甲乙两家服装店优惠活动如下表:
日开业,商场内两家服装店举行开业大酬宾活动,甲乙两家服装店优惠活动如下表:
购买服装总金额(元) | 不超过 | 超过 |
|
优惠幅度 | 打 | 打 | 打 |
乙服装店优惠活动:购买服装总金额每满![]() 元减
元减![]() 元.
元.
例如:购买总金额满![]() 元减
元减![]() 元,满
元,满![]() 元减
元减![]() 元,以此类推.
元,以此类推.
(1)若在两家店购买服装总金额都是![]() 元,哪家店实际付款更少?少多少?
元,哪家店实际付款更少?少多少?
(2)若购买服装总金额小于![]() 元,选择哪家店购买服装更划算?请通过计算说明理由.
元,选择哪家店购买服装更划算?请通过计算说明理由.