Question

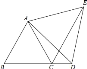
【题目】如图1，在长方形中，，有一只蚂蚁在点 处开始以每秒1个单位的速度沿边向点爬行，另一只蚂蚁从点以每秒2个单位的速度沿边向点爬行，蚂蚁的大小忽略不计，如果、同时出发，设运动时间为s.

(1)当时，求的面积;

(2)当 时，试说明是直角二角形;

(3)当运动3s时，点停止运动，点以原速立即向点返回，在返回的过程中，是否存在点，使得平分?若存在，求出点运动的时间，若不存在请说明理由.

Answer 1

【答案】（1）8；（2）详见解析；（3）存在点Q，使得DP平分，此时s

【解析】

（1）根据题意求出t=2时PB和BQ的长，然后根据三角形面积公式即可求出面积；

（2）利用勾股定理求出DP，PQ，DQ，得到即可证明；

（3）根据题意得到AP=3，设Q再运动x秒，用x表示出BQ，CQ，作PH⊥BC于H，可证，求出DQ，最后在Rt△DCQ中利用勾股定理建立方程解出x，然后加上3秒，即为Q的运动时间.

（1）当时，

S△ABD =×4×4=8

（2）当时，

∴

∴

∵∠DQP=90°,

∴是直角三角形.

(3) 当时，，∴P是AB的中点，PA=PB=3，

此时BQ=6，设点Q返回时再运动x秒符合要求，则

作PH⊥BC于H，∵PD平分∠ADQ，又∵PA⊥AD，

在Rt△PBQ和Rt△PHQ中，PQ=PQ，PB=PH，

，

在Rt△DCQ中，

解得

所以Q的运动时间为秒

答：存在点，使得平分，此时Q点运动时间为秒.