Question

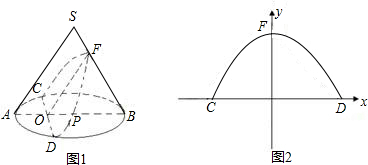
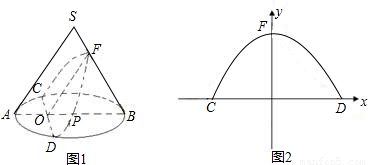
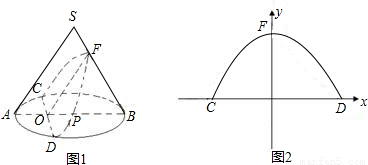
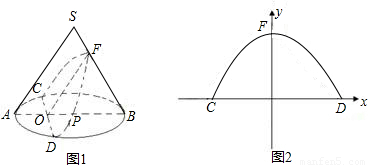
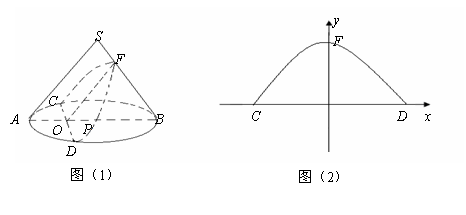
聪明好学的小云查阅有关资料发现：用不过圆锥顶点平行于一条母线的平面截圆锥所得的截面为抛物面，即图（1）中曲线CFD为抛物线的一部分，如图（1），圆锥体SAB的母线长为10，侧面积为50，圆锥的截面CFD交母线SB于F，交底面⊙P于C、D，AB⊥CD于O，OF∥SA且OF⊥CD，OP＝4．

（1）求底面圆的半径AP的长及圆锥侧面展开图的圆心角的度数；

（2）当以CD所在直线为x轴，OF所在的直线为y轴建立如图（2）所示的直角坐标系，求过C、F、D三点的抛物线的函数关系式．

 

Answer 1

 (1) ∵50=·AP·10  ∴AP=5          （2分）

∵2·5=  ∴n=180⁰          （2分）                     

(2)y=ax²＋c

由OF∥SA得△OFB∽△ASB， ∴=  ∴=

∴OF=9   ∴F（0,9）

连结AC，BC，可得CO²=1×9，∴CO=3  ∴C（-3,0），

再代入到y=ax²＋c中，得a＝-1

∴y= -x²+9                        （4分）