题目内容
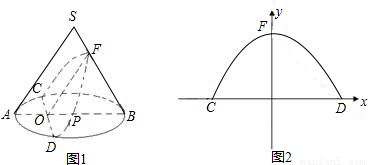
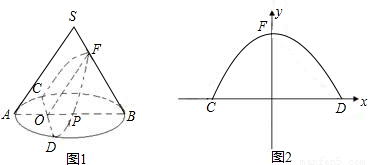
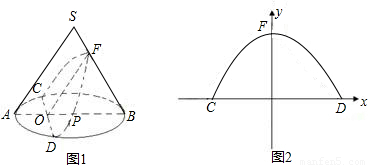
聪明好学的小云查阅有关资料发现:用不过圆锥顶点平行于一条母线的平面截圆锥所得的截面为抛物面,即图1中曲线CFD为抛物线的一部分,如图1,圆锥体SAB的母线长为10,侧面积为50π,圆锥的截面CFD交母线SB于F,交底面⊙P于C、D,AB⊥CD于O,OF∥SA且OF⊥CD,OP=4,OB=9.(1)求底面圆的半径AP的长及圆锥侧面展开图的圆心角的度数;
(2)当以CD所在直线为x轴,OF所在的直线为y轴建立如图2所示的直角坐标系,求过C、F、D三点的抛物线的函数关系式.
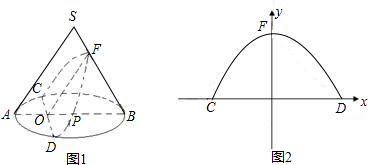
分析:(1)根据圆锥侧面积的计算方法即可求得底面圆半径AP的长;由于圆锥侧面展开图是个扇形,且弧长等腰底面圆的周长,可据此求出侧面展开图的圆心角的度数;
(2)根据(1)得出的底面圆的半径即可得到BO、AB的长,由于OF∥AS,易证得△OBF∽△ABS,根据相似三角形所得到的比例线段即可求得OF的长,由此可得到F点的坐标;连接AC、BC;根据圆周角定理知∠ACB=90°,在Rt△ACB中,OC⊥AB,根据射影定理即可求出OC的长,由此可得到C点的坐标;根据C、F的坐标,即可用待定系数法求出抛物线的解析式.
(2)根据(1)得出的底面圆的半径即可得到BO、AB的长,由于OF∥AS,易证得△OBF∽△ABS,根据相似三角形所得到的比例线段即可求得OF的长,由此可得到F点的坐标;连接AC、BC;根据圆周角定理知∠ACB=90°,在Rt△ACB中,OC⊥AB,根据射影定理即可求出OC的长,由此可得到C点的坐标;根据C、F的坐标,即可用待定系数法求出抛物线的解析式.
解答:解:(1)∵50π=π•AP•10
∴AP=5;
∵2π•5=
∴n=180°;
故底面圆的半径长为5,侧面展开图的圆心角的度数为180°;
(2)由OF∥SA得△OFB∽△ASB,
∴
=
,
∴
=
∴OF=9,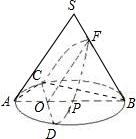
∴F(0,9);
连接AC,BC,则∠ACB=90°;
Rt△ABC中,OC⊥AB,OA=1,OB=9;
由射影定理可得CO2=1×9,
∴CO=3,
∴C(-3,0);
设抛物线的解析式为:y=ax2+c,则有:
,
解得
;
∴抛物线的解析式为:y=-x2+9.
∴AP=5;
∵2π•5=
| 10nπ |
| 180 |
∴n=180°;
故底面圆的半径长为5,侧面展开图的圆心角的度数为180°;
(2)由OF∥SA得△OFB∽△ASB,
∴
| OF |
| SA |
| BO |
| AB |
∴
| OF |
| 10 |
| 9 |
| 10 |
∴OF=9,

∴F(0,9);
连接AC,BC,则∠ACB=90°;
Rt△ABC中,OC⊥AB,OA=1,OB=9;
由射影定理可得CO2=1×9,
∴CO=3,
∴C(-3,0);
设抛物线的解析式为:y=ax2+c,则有:
|
解得
|
∴抛物线的解析式为:y=-x2+9.
点评:此题主要考查了二次函数解析式的确定、相似三角形的性质以及圆锥的相关计算,需要牢记的内容是圆锥的侧面积计算方法:S=πRL(R为底面圆半径,L为圆锥的母线长).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目