题目内容
O是△ABC的内心,∠BOC为130°,则∠A的度数为
- A.130°
- B.60°
- C.70°
- D.80°
D
分析:根据题意画出图形,由三角形内切定义可知:OB、OC是∠ABC、∠ACB的角平分线.利用内角和定理先求得∠OBC+∠OCB=80°,所以可知∠OBC+∠OCB= (∠ABC+∠ACB),把对应数值代入此关系式即可求得∠A的值.
(∠ABC+∠ACB),把对应数值代入此关系式即可求得∠A的值.
解答: 解:如图所示:∵OB、OC是∠ABC、∠ACB的角平分线,
解:如图所示:∵OB、OC是∠ABC、∠ACB的角平分线,
∴∠OBC+∠OCB=180°-∠BOC=180°-130°=50°,
∴∠OBC+∠OCB= (∠ABC+∠ACB)=50°,
(∠ABC+∠ACB)=50°,
∴∠ABC+∠ACB=100°,
∴∠A=180°-100°=80°.
故选D.
点评:本题考查的是三角形的内切圆与内心,熟知三角形的内心就是三角形三个内角角平分线的交点是解答此题的关键.
分析:根据题意画出图形,由三角形内切定义可知:OB、OC是∠ABC、∠ACB的角平分线.利用内角和定理先求得∠OBC+∠OCB=80°,所以可知∠OBC+∠OCB=
 (∠ABC+∠ACB),把对应数值代入此关系式即可求得∠A的值.
(∠ABC+∠ACB),把对应数值代入此关系式即可求得∠A的值.解答:
 解:如图所示:∵OB、OC是∠ABC、∠ACB的角平分线,
解:如图所示:∵OB、OC是∠ABC、∠ACB的角平分线,∴∠OBC+∠OCB=180°-∠BOC=180°-130°=50°,
∴∠OBC+∠OCB=
 (∠ABC+∠ACB)=50°,
(∠ABC+∠ACB)=50°,∴∠ABC+∠ACB=100°,
∴∠A=180°-100°=80°.
故选D.
点评:本题考查的是三角形的内切圆与内心,熟知三角形的内心就是三角形三个内角角平分线的交点是解答此题的关键.

练习册系列答案
相关题目
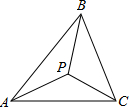 如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB的度数为( )
如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB的度数为( )| A、150° | B、120° | C、90° | D、60° |
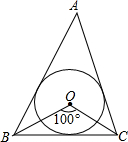 如图所示,O是△ABC的内心,∠BOC=100°,则∠BAC=
如图所示,O是△ABC的内心,∠BOC=100°,则∠BAC=
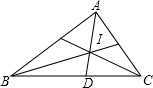 如图,I是△ABC的内心,∠A=40°,则∠CIB=
如图,I是△ABC的内心,∠A=40°,则∠CIB= 如图,AB是圆O的直径,AB=10,点C是圆O上一动点(与A,B不重合),∠ACB的平分线交圆O于D.
如图,AB是圆O的直径,AB=10,点C是圆O上一动点(与A,B不重合),∠ACB的平分线交圆O于D.