题目内容
18、(1)是否有满足方程x2-y2=1998的整数解x和y?如果有,求出方程的解;如果没有,说明理由.
(2)一个立方体的顶点标上+1或一1,面上标上一个数,它等于这个面的4个顶点处的数的乘积,这样所标的14个数的和能否为0?
(2)一个立方体的顶点标上+1或一1,面上标上一个数,它等于这个面的4个顶点处的数的乘积,这样所标的14个数的和能否为0?
分析:(1)x2-y2=(x+y)(x-y)因为(x+y),(x-y)同奇偶所以(x+y)(x-y)要末是奇数,要末是4的倍数但1998被4除余2如果所标的14个数的和能否为0.则有7个+1,7个-1.但可以知道,1个面有5个数,无论怎么放,都只有2或4个-1.所以不可能出现7个-1.所标的14个数的和不能为0.
解答:解:(1)x2-y2=1998,1998=2×3×3×3×37
若x,y同为偶数,则(x+y),(x-y)同为偶数,→(x+y)(x-y)=4×…不合
若x,y同为奇数,则(x+y),(x-y)同为偶数,→(x+y)(x-y)=4×…不合
若x,y一奇一偶,则(x+y),(x-y)同为奇数,→(x+y)(x-y)=不含因数2
∴方程x2-y2=1998没有整数解.
9992-9982=(999+998)(999-998)=1997×1=1997
10002-9992=(1000+999)(1000-999)=1999×1=1999
1997<;1998<;1999,
∴方程x2-y2=1998没有整数解
解:(2)所标的14个数的和能否为0.则有7个+1,7个-1.但可以知道,1个面有5个数,无论怎么放,都只有2或4个-1.
所以不可能出现7个-1.
故:所标的14个数的和不能为0.
若x,y同为偶数,则(x+y),(x-y)同为偶数,→(x+y)(x-y)=4×…不合
若x,y同为奇数,则(x+y),(x-y)同为偶数,→(x+y)(x-y)=4×…不合
若x,y一奇一偶,则(x+y),(x-y)同为奇数,→(x+y)(x-y)=不含因数2
∴方程x2-y2=1998没有整数解.
9992-9982=(999+998)(999-998)=1997×1=1997
10002-9992=(1000+999)(1000-999)=1999×1=1999
1997<;1998<;1999,
∴方程x2-y2=1998没有整数解
解:(2)所标的14个数的和能否为0.则有7个+1,7个-1.但可以知道,1个面有5个数,无论怎么放,都只有2或4个-1.
所以不可能出现7个-1.
故:所标的14个数的和不能为0.
点评:此题考查了学生对数的奇偶性问题的掌握.关键是深刻理解奇偶数的意义.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
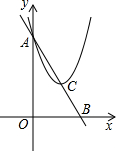 x2+bx+c的图象经过点A和点C,点C是二次函数图象上的最低点,并且满足AC=2BC
x2+bx+c的图象经过点A和点C,点C是二次函数图象上的最低点,并且满足AC=2BC