题目内容
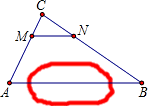 如图,A,B两点被池塘隔开,在AB外任选一点C,连接AC,BC,分别取其三等分点M,N,量得MN=30m,若CN<NB,CM<MA,则AB的长是
如图,A,B两点被池塘隔开,在AB外任选一点C,连接AC,BC,分别取其三等分点M,N,量得MN=30m,若CN<NB,CM<MA,则AB的长是
- A.60m
- B.120m
- C.180m
- D.90m
D
分析:先根据M、N分别是AC与BC的三等分点且CN<NB,CM<MA可知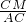 =
= =
= ,故可得出△MNC∽△ABC,由MN=30m即可求出AB的长.
,故可得出△MNC∽△ABC,由MN=30m即可求出AB的长.
解答:∵M、N分别是AC与BC的三等分点且CN<NB,CM<MA,
∴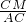 =
= =
= ,
,
∵∠C是公共角,
∴△MNC∽△ABC,
∴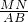 =
=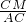 =
= ,即
,即 =
= ,解得AB=90m.
,解得AB=90m.
故选D.
点评:本题考查的是相似三角形的应用,先根据题意判断出△MNC∽△ABC是解答此题的关键.
分析:先根据M、N分别是AC与BC的三等分点且CN<NB,CM<MA可知
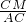 =
= =
= ,故可得出△MNC∽△ABC,由MN=30m即可求出AB的长.
,故可得出△MNC∽△ABC,由MN=30m即可求出AB的长.解答:∵M、N分别是AC与BC的三等分点且CN<NB,CM<MA,
∴
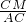 =
= =
= ,
,∵∠C是公共角,
∴△MNC∽△ABC,
∴
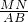 =
=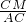 =
= ,即
,即 =
= ,解得AB=90m.
,解得AB=90m.故选D.
点评:本题考查的是相似三角形的应用,先根据题意判断出△MNC∽△ABC是解答此题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 如图,将一等边三角形剪去一个角后,∠1+∠2=
如图,将一等边三角形剪去一个角后,∠1+∠2=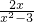 的值是
的值是 小莉站在离一棵树水平距离为a米的地方,用一块含30°的直角三角板按如图所示的方式测量这棵树的高度,已知小莉的眼睛离地面的高度是1.5米,那么她测得这棵树的高度为
小莉站在离一棵树水平距离为a米的地方,用一块含30°的直角三角板按如图所示的方式测量这棵树的高度,已知小莉的眼睛离地面的高度是1.5米,那么她测得这棵树的高度为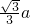 )米
)米 a)米
a)米