Question

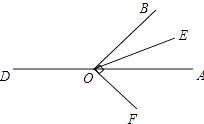
【题目】O为直线DA上一点，OB⊥OF，EO是∠AOB的平分线．

（1）如图（1），若∠AOB=130°，求∠EOF的度数；
（2）若∠AOB=α，90°＜α＜180°，求∠EOF的度数；
（3）若∠AOB=α，0°＜α＜90°，请在图（2）中画出射线OF，使得（2）中∠EOF的结果仍然成立．

Answer 1

【答案】
（1）解：∵∠AOB=130°，EO是∠AOB的平分线，
∴ =65°，
∵OB⊥OF，
∴∠BOF=90°，
∴∠AOF=∠AOB﹣∠BOF=130°﹣90°=40°，
∴∠EOF=∠AOE﹣∠AOF=65°﹣40°=25°
（2）解：∵∠AOB=α，90°＜α＜180°，EO是∠AOB的平分线，
∴∠AOE= ，
∵∠BOF=90°，
∴∠AOF=α﹣90°，
∴∠EOF=∠AOE﹣∠AOF= ﹣（α﹣90°）=90
（3）解：如图，∵∠AOB=α，0°＜α＜90°，
∴∠BOE=∠AOE= ，
∵∠BOF=90°，
∴∠EOF=∠BOF﹣∠BOE=90 ．

【解析】（1）根据已知条件EO是∠AOB的平分线可求∠AOE，∠EOF的构成，∠EOF=∠AOE﹣∠AOF可求解；（2）同（1）；（3）同（1）.