题目内容
如图,AC⊥BD于点E,E为AC上的一点,且∠CBA=45°,AD=BE.
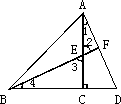
求证:BF⊥AD.
答案:
解析:
解析:
|
分析:要证明BF⊥AD,只要证明∠AFE=90°,即只要说明∠1+∠2=90°.由题意,易知∠3+∠4=90°,∠2=∠3,那么只要证明∠1=∠4,应考虑∠1和∠4所在的△ACD和△BCE全等.在这两个三角形中,AD=BE,∠ACD=∠BCE=90°.结合已知条件,只需证明CA=CB即可. 证明:因为AC⊥BD,所以∠ACB=∠ACD=90°. 又因为∠CBA=45°, 所以△ABC是等腰直角三角形. 所以CA=CB. 在Rt△ACD和Rt△BCE中, 因为 所以△ACD≌△BCE.(HL) 所以∠1=∠4. 又因为∠3+∠4=90°,∠2=∠3, 所以∠1+∠2=90°. 所以∠AFE=90°,即BF⊥AD. 点评:三角形全等的判定在解决三角形的问题中具有重要作用,尤其是解答与线段相等、与角相等的一些问题等.同学们在解题的过程中一定要注意选择合适的判定三角形全等的条件. |

练习册系列答案
相关题目
 12、如图,AC⊥BD于点C,DE⊥AB于点E,且AB=6,DB=8,则S△ABC:S△DBE=
12、如图,AC⊥BD于点C,DE⊥AB于点E,且AB=6,DB=8,则S△ABC:S△DBE=