题目内容
在数学的学习中,我们要学会总结,不断地归纳,思考和运用,这样才能提高我们解决问题的能力,下面这个问题大家一定似曾相识:(1)比较大小:
①2+1
| 2×1 |
| 1 |
| 3 |
3×
|
| 8×8 |
通过上面三个计算,我们可以初步对任意的非负实数a,b做出猜想a+b
| ab |
(2)学习了《二次根式》后我们可以对此猜想进行代数证明,请欣赏:
对于任意非负实数a,b,∵(
| a |
| b |
| ab |
| ab |
(3)学习《圆》后,我们可以对这个结论进行几何验证:
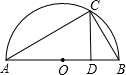
如图,AB为半圆O的直径,C为半圆上的任意一点,(与A、B不重合)过点C作CD⊥AB,垂足为D,AD=a,DB=b.
根据图形证明:a+b≥2
| ab |
(4)蓦然回首,我们发现在上学期的《梯形的中位线》一节遇到的一个问题,此时运用这个结论解决是那样的简单:
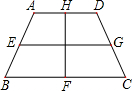
如图有一个等腰梯形工件(厚度不计),其面积为1800cm2,现在要用细包装带如图那样包扎(四点为四边中点),则至少需要包装带的长度为
(注意:包扎时背面也有带子,打结处长度忽略不计)
分析:(1)直接计算算式,比较大小即可;
(3)连接OC,证明△ABC为直角三角形,CD⊥AB,利用相似三角形的性质可证CD=
,而OC=
AB=
(a+b),由图可知OC≥CD,代入证明结论;
(4)设EG=a,FH=b,根据梯形面积公式可知ab=1800,再由a+b≥2
,可求a+b的最小值,得出包装带的长度.
(3)连接OC,证明△ABC为直角三角形,CD⊥AB,利用相似三角形的性质可证CD=
| ab |
| 1 |
| 2 |
| 1 |
| 2 |
(4)设EG=a,FH=b,根据梯形面积公式可知ab=1800,再由a+b≥2
| ab |
解答:解:(1)>,>,=,≥;
(3)连接OC,∵AB是直径,
∴∠ACB=90°,
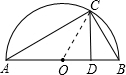
∴a+b=AD+BD=AB=2OC,
又∵CD⊥AB,
∴∠ACB=∠CDB=90°,
∵∠CAB+∠ABC=90°,∠DCB+∠ABC=90°,
∴∠CAB=∠DCB,
∴△CDB∽△ADC,
∴AD•BD=CD2,
即ab=CD2,∴CD=
,
而OC≥CD,
∴a+b≥2
,
当D与O重合即CD为半径时等号成立.
(4)设EG=a,FH=b,
根据梯形面积公式可知ab=1800,
∵a+b≥2
=2
=60
,
∴a+b的最小值为60
,
∴包装带需要2(a+b)=120
cm.
故答案为:120
.
(3)连接OC,∵AB是直径,
∴∠ACB=90°,

∴a+b=AD+BD=AB=2OC,
又∵CD⊥AB,
∴∠ACB=∠CDB=90°,
∵∠CAB+∠ABC=90°,∠DCB+∠ABC=90°,
∴∠CAB=∠DCB,
∴△CDB∽△ADC,
∴AD•BD=CD2,
即ab=CD2,∴CD=
| ab |
而OC≥CD,
∴a+b≥2
| ab |
当D与O重合即CD为半径时等号成立.
(4)设EG=a,FH=b,
根据梯形面积公式可知ab=1800,
∵a+b≥2
| ab |
| 1800 |
| 2 |
∴a+b的最小值为60
| 2 |
∴包装带需要2(a+b)=120
| 2 |
故答案为:120
| 2 |
点评:本题考查了相似三角形的判定与实际应用.关键是由易到难,由特殊到一般,逐步求证,并会运用所得不等式解决实际问题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 ; ②
; ②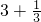 ______
______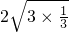 ③8+8______
③8+8______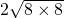
 ;
;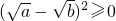 ,∴
,∴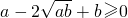 ,∴
,∴ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.


 ; ②
; ② ______
______ ③8+8______
③8+8______
 ;
; ,∴
,∴ ,∴
,∴ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立. ,并指出等号成立时的条件.
,并指出等号成立时的条件.