题目内容
【题目】已知二次函数y=![]() x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
x2+bx+c的图象经过点A(﹣3,6),并与x轴交于点B(﹣1,0)和点C,与y轴交于点E,顶点为P,对称轴与x轴交于点D
(Ⅰ)求这个二次函数的解析式;
(Ⅱ)连接CP,△DCP是什么特殊形状的三角形?并加以说明;
(Ⅲ)点Q是第一象限的抛物线上一点,且满足∠QEO=∠BEO,求出点Q的坐标.
【答案】(Ⅰ)二次函数解析式为y=![]() x2﹣x﹣
x2﹣x﹣![]() ;(Ⅱ)△DCP是等腰直角三角形,理由见解析;(Ⅲ)点Q坐标为(5,6).
;(Ⅱ)△DCP是等腰直角三角形,理由见解析;(Ⅲ)点Q坐标为(5,6).
【解析】
(Ⅰ)把A(-3,6),B(-1,0)代入y=![]() x2+bx+c,解方程组即可解决问题.
x2+bx+c,解方程组即可解决问题.
(Ⅱ)结论:△DCP是等腰直角三角形.求出C、D、E三点坐标即可解决问题.
(Ⅲ)如图,连接BE、DE.只要证明△EOB≌△EOD,得到∠DEO=∠BEO,所以直线DE与抛物线的交点即为所求的点Q.求出直线DE的解析式,解方程组即可.
(Ⅰ)把A(﹣3,6),B(﹣1,0)代入y=![]() x2+bx+c,
x2+bx+c,
得到 ,
,
解得 ,
,
∴二次函数解析式为y=![]() x2﹣x﹣
x2﹣x﹣![]() .
.
(Ⅱ)结论:△DCP是等腰直角三角形.
理由:对于抛物线y=![]() x2﹣x﹣
x2﹣x﹣![]() ,令y=0,则
,令y=0,则![]() x2﹣x﹣
x2﹣x﹣![]() =0,解得x=﹣1或3,
=0,解得x=﹣1或3,
∴点C坐标(3,0),
令x=0则y=﹣![]() ,
,
∴点E坐标(0,﹣![]() ),
),
∵y=![]() x2﹣x﹣
x2﹣x﹣![]() =
=![]() (x﹣1)2﹣2,
(x﹣1)2﹣2,
∴顶点P坐标(1,﹣2),点D坐标(1,0),
∴CD=PD=2,
∵∠PDC=90°,
∴△PDC是等腰直角三角形.
(Ⅲ)如图,连接BE、DE.

∵B(﹣1,0),D(1,0),E(0,﹣![]() ),
),
∴OB=OD,OE=OE,∠BOE=∠DOE,
∴△EOB≌△EOD,
∴∠DEO=∠BEO,
∴直线DE与抛物线的交点即为所求的点Q.
设直线DE的解析式为y=kx+b,则有 ,
,
解得 ,
,
∴直线DE的解析式为y=![]() ,
,
由 解得
解得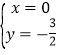 或
或![]() ,
,
∴点Q坐标为(5,6).

【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
摸到白球的频率 | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.01);
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球,这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.