题目内容
 如图,AB切⊙O于点B,AD过圆心,且与⊙O相交于C、D两点,连接BD,若⊙O的半径为1,AO=2CO,则BD的长度为________.
如图,AB切⊙O于点B,AD过圆心,且与⊙O相交于C、D两点,连接BD,若⊙O的半径为1,AO=2CO,则BD的长度为________.

分析:如图:连接OB,过点O作OE⊥BD于点E;根据切线的性质知道∠ABO=90°,由OB=OC=OD,AO=2CO得到AO=2BO,进一步得到∠A=30°,∠AOB=60°,所以∠D=30°;而⊙O的半径为1,再根据垂径定理和三角函数可以求出ED,BD.
解答:
 解:如图:
解:如图:连接OB,过点O作OE⊥BD于点E;
∵AB切⊙O于点B,
∴∠ABO=90°;
∵OB=OC=OD,AO=2CO,
∴AO=2BO,∠D=∠OBD,
∴∠A=30°,
∴∠AOB=60°,
∴∠D=30°;
∵⊙O的半径为1,
∴OE=
 ,ED=
,ED= ,
,∴BD=
 .
.故填空答案:BD=
 .
.点评:此题考查了:
①圆的切线垂直于过切点的半径;
②直角三角形的性质,直角三角形中,如果一个直角边等于斜边的一半,那么它所对的锐角等于30°;
此外解题时要注意辅助线的作法.

练习册系列答案
相关题目
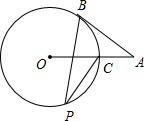 已知:如图,AB切⊙O于点B,OA与⊙O交于点C,点P在⊙O上,若∠BAC=40°,则∠BPC的度数为( )
已知:如图,AB切⊙O于点B,OA与⊙O交于点C,点P在⊙O上,若∠BAC=40°,则∠BPC的度数为( )| A、20° | B、25° | C、30° | D、40° |
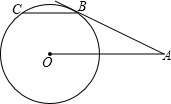 如图,AB切⊙O于点B,OA=2
如图,AB切⊙O于点B,OA=2| 3 |
A、
| ||||
B、
| ||||
| C、π | ||||
D、
|
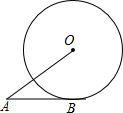 如图,AB切⊙O于点B,AB=4cm,AO=6cm,则⊙O的半径为
如图,AB切⊙O于点B,AB=4cm,AO=6cm,则⊙O的半径为 (2012•西藏)如图,AB切⊙O于点B,延长AO交⊙O于点C,连接BC.若∠A=40°,则∠C=( )
(2012•西藏)如图,AB切⊙O于点B,延长AO交⊙O于点C,连接BC.若∠A=40°,则∠C=( ) (2012•广东模拟)如图,AB切⊙O于点A,OD⊥弦AC于点D,延长OD,交AB于点B,若∠O=60°,AC=6cm,则AB=
(2012•广东模拟)如图,AB切⊙O于点A,OD⊥弦AC于点D,延长OD,交AB于点B,若∠O=60°,AC=6cm,则AB=