题目内容
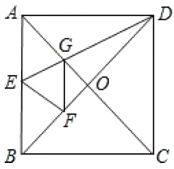
【题目】如图,正方形![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,折叠正方形纸片,使
,折叠正方形纸片,使![]() 落在
落在![]() 上,点
上,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合,展开后折痕
重合,展开后折痕![]() 分别交
分别交![]() 于点
于点![]() ,连
,连![]() 给出下列结论,其中正确的个数有( )
给出下列结论,其中正确的个数有( )
①![]() ;②
;②![]() ;③四边形
;③四边形![]() 是菱形;④
是菱形;④![]() .
.
A.1个B.2个C.3个D.4个
【答案】B
【解析】
①由ABCD是正方形,可得到三角形ACD是等腰直角三角形,则可以得到![]() 的度数;
的度数;
②证![]() ,得AG=FG,由FG>OG即可得;
,得AG=FG,由FG>OG即可得;
③证四边形![]() 四边的关系,再判断是否是菱形;
四边的关系,再判断是否是菱形;
④设OA=a,证![]() ,得
,得![]() ,易得
,易得![]() ,类似可得
,类似可得![]() ,即可得到OF与BF的关系.
,即可得到OF与BF的关系.
解:①∵ABCD是正方形
∴三角形ACD是等腰直角三角形
因此![]()
故①错误;
② 由折叠性质可得:AE=EF, ![]() ,
,
在![]() 和
和![]() 中,
中,
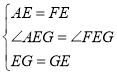
∴![]() (SAS)
(SAS)
∴AG=FG
∵在直角三角形GOF中,AG=FG>GO,
∴![]()
故②错误;
③ ∵![]() ,
,
![]() ,
,
∴![]()
∴ AE=AG,
又∵AE=FE,AG=FG,
∴AE=EF=GF=AG,
∴四边形![]() 是菱形
是菱形
故③正确;
④ 设OF=a
∵由②的解析过程知道![]()
∴![]() ,
,
又∵![]() ,
,
∴![]()
∵在直角三角形OFG中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵在直角三角形EBF中,![]() ,
,
即![]() ,
,
故④正确;
综上,只有③④两个正确,故选B.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目