题目内容
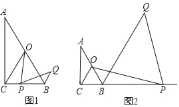
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)如图1,当点P在线段BC上时,试猜想写出线段CP与BQ的数量关系,并证明你的猜想;
(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?(直接写“成立”或“不成立”即可,不需证明).
【答案】(1) BQ=CP.理由见解析;(2) 成立:PC=BQ, 理由见解析.
【解析】
(1)由∠ACB=90°,∠A=30°得到∠ABC=60°,根据直角三角形斜边上中线性质得到OB=OC,则可判断△OCB、△CPH为等边三角形,作辅助线PH∥AB交CO于H,证明△POH≌△QPB全等可得PH=QB= PC;
(2)与(1)的证明方法同样得到△POH≌△QPB,可得PH=QB= PC。
解:(1)结论:BQ=CP.
理由:如图1中,作PH∥AB交CO于H.

在Rt△ABC中,∵∠ACB=90°,∠A=30°,点O为AB中点,
∴CO=AO=BO,∠CBO=60°,
∴△CBO是等边三角形,
∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°,
∴∠CHP=∠CPH=60°,
∴△CPH是等边三角形,
∴PC=PH=CH,
∴OH=PB,
∵∠OPB=∠OPQ+∠QPB=∠OCB+∠COP,
∵∠OPQ=∠OCP=60°,
∴∠POH=∠QPB,
∵在△POH与△QPB中
![]() ,
,
∴△POH≌△QPB(SAS),
∴PH=QB,
∴PC=BQ.
(2)成立:PC=BQ.

理由:作PH∥AB交CO的延长线于H.
在Rt△ABC中,∵∠ACB=90°,∠A=30°,点O为AB中点,
∴CO=AO=BO,∠CBO=60°,
∴△CBO是等边三角形,
∴∠CHP=∠COB=60°,∠CPH=∠CBO=60°,
∴∠CHP=∠CPH=60°,
∴△CPH是等边三角形,
∴PC=PH=CH,
∴OH=PB,
∵∠POH=60°+∠CPO,∠QPO=60°+∠CPQ,
∴∠POH=∠QPB,
∵在△POH与△QPB中
![]() ,
,
∴△POH≌△QPB(SAS),
∴PH=QB,
∴PC=BQ.