Question

【题目】如图，⊙O的直径为AB，点C在圆周上（异于A，B），AD⊥CD．

（1）若BC=3，AB=5，求AC的值；
（2）若AC是∠DAB的平分线，求证：直线CD是⊙O的切线．

Answer 1

【答案】
（1）

解：∵AB是⊙O直径，C在⊙O上，

∴∠ACB=90°，

又∵BC=3，AB=5，

∴由勾股定理得AC=4

（2）

解：证明：

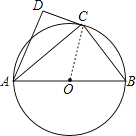
∵AC是∠DAB的角平分线，

∴∠DAC=∠BAC，

又∵AD⊥DC，

∴∠ADC=∠ACB=90°，

∴△ADC∽△ACB，

∴∠DCA=∠CBA，

又∵OA=OC，

∴∠OAC=∠OCA，

∵∠OAC+∠OBC=90°，

∴∠OCA+∠ACD=∠OCD=90°，

∴DC是⊙O的切线

【解析】（1）首先根据直径所对的圆周角为直角得到直角三角形，然后利用勾股定理求得AC的长即可；（2）连接OC，证OC⊥CD即可；利用角平分线的性质和等边对等角，可证得∠OCA=∠CAD，即可得到OC∥AD，由于AD⊥CD，那么OC⊥CD，由此得证．此题主要考查的是切线的判定方法．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．