题目内容
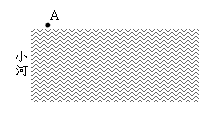
在数学综合实践活动课上,老师只给各活动小组教学用直角三角板一个、皮尺一条(皮 尺长度不够直接测河宽),测量如下图所示小河的宽度(A为河岸边一棵柳树).
尺长度不够直接测河宽),测量如下图所示小河的宽度(A为河岸边一棵柳树).
(1)简要说明你的测量方法,并在右图中画出图形;
(2)说明你作法的合理性.
 解:(1)测量方法:
解:(1)测量方法:①在不同于A点的对岸作直线MN;
②用观测法作AB⊥MN;
③在直线MN取两点C、D,使BC=CD;
④过D作DE⊥MN,使A、C、E三点共线,则DE的长度即为河宽.
(2)在Rt△ABC和Rt△EDC中,
∠ABC=∠EDC=90°,BC=CD,∠ACB=∠ECD,
∴Rt△ABC≌Rt△EDC.
∴AB=ED.
分析:已知等边及垂直,在直角三角形中,可考虑ASA证明三角形全等,从而推出线段相等.
点评:本题考查全等三角形的应用.在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 22、在数学综合实践活动课上,老师只给各活动小组教学用直角三角板一个、皮尺一条(皮尺长度不够直接测河宽),测量如下图所示小河的宽度(A为河岸边一棵柳树).
22、在数学综合实践活动课上,老师只给各活动小组教学用直角三角板一个、皮尺一条(皮尺长度不够直接测河宽),测量如下图所示小河的宽度(A为河岸边一棵柳树).