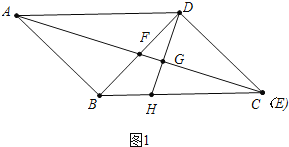
题目内容
【题目】已知,在![]() 中,
中,![]() 为射线
为射线![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() .
.
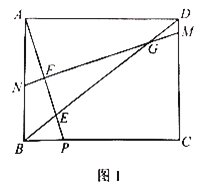
(1)如图1,若![]() 点与点
点与点![]() 重合,且
重合,且![]() ,求
,求![]() 的长;
的长;
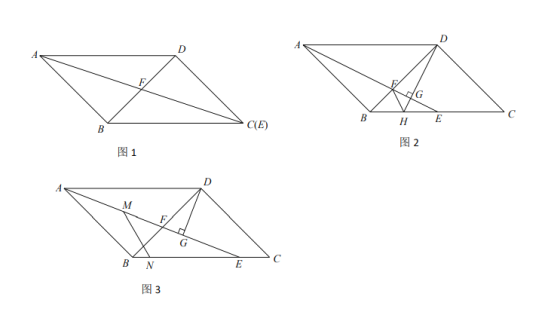
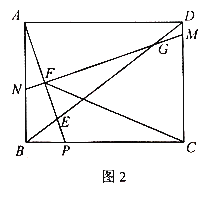
(2)如图2,当点![]() 在
在![]() 边上时,过点
边上时,过点![]() 作
作![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .求证:
.求证:![]() .
.
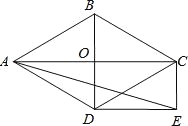
(3)如图3,当点![]() 在射线
在射线![]() 上运动时,过点
上运动时,过点![]() 作
作![]() 于
于![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 边上且
边上且![]() ,已知
,已知![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)如图1中,利用等腰三角形的性质可得![]() ,利用平行四边形的性质可得
,利用平行四边形的性质可得![]() 为
为![]() 中点,在
中点,在![]() 中,由勾股定理可求得
中,由勾股定理可求得![]() ,则可求得
,则可求得![]() ,在
,在![]() 中,再利用勾股定理可求得
中,再利用勾股定理可求得![]() ;
;
(2)如图2中,在![]() 上截取
上截取![]() ,连接
,连接![]() ,可先证明
,可先证明![]() ,再证明
,再证明![]() ,可证得结论;
,可证得结论;
(3)连接![]() 并延长到
并延长到![]() ,使
,使![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,得到
,得到![]() ,于是得到点
,于是得到点![]() 的轨迹是以
的轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的弧,且
为半径的弧,且![]() ,求得
,求得![]() 最小值为6,根据三角形的中位线定理即可得到结论.
最小值为6,根据三角形的中位线定理即可得到结论.
(1)![]()
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 当点
当点![]() 与点
与点![]() 重合时,
重合时,![]()
在![]() 中,
中,![]()
![]()
![]()
![]() 中,
中,![]() .
.
(2)证明:如图2中,在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,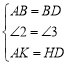 ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
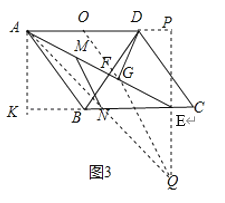
![]() 解:连接
解:连接![]() 并延长到
并延长到![]() ,使
,使![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,作AK⊥BC,交BC延长线于点K,作QP⊥AD,交AD延长线于点P.
,作AK⊥BC,交BC延长线于点K,作QP⊥AD,交AD延长线于点P.
![]() ,
,
![]() 点
点![]() 的轨迹是以
的轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的弧,且
为半径的弧,且![]() ,
,
根据△ABD为等腰直角三角形,可得AD=![]() ,
,
∴AO=![]() ,
,
根据△ABK为等腰直角三角形,可得AK=BK=4,可得QE=PE=4,
∴PQ=8,
∵BK=4,BN=1,
∴KN=5,
∴KE=AP=10,
∴OP=6,
![]() ,
,![]() ,
,
![]() 最小值为6,
最小值为6,
![]() 是
是![]() 的中位线,
的中位线,
![]() 的最小值为3.
的最小值为3.

 名校课堂系列答案
名校课堂系列答案【题目】本学期,大兴区开展了“恰同学少年,品诗词美韵”中华传统诗词大赛活动![]() 小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
诗词数量 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
人数 | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
那么这30名同学四月份诗词背诵数量的众数和中位数分别是![]()
![]()
A. 11,7 B. 7,5 C. 8,8 D. 8,7