题目内容
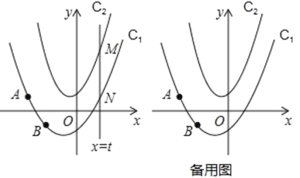
【题目】如图,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.
(1)求抛物线C1的表达式;
(2)直接用含t的代数式表达线段MN的长;
(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值.
【答案】(1)y=x2+x﹣1;(2)MN=t2+2;(3)t=0或1
【解析】
(1)将点A、B的坐标代入抛物线表达式,即可求解;
(2)点M、N的坐标分别为:(t,2t2+t+1)、(t,t2+t-1),即可求解;
(3)分∠ANM=90°、∠AMN=90°两种情况,分别求解即可.
解:(1)将点A、B的坐标代入抛物线表达式得:![]() ,解得:
,解得:![]() ,
,
故抛物线C1的表达式为:y=x2+x﹣1;
(2)点M、N的坐标分别为:(t,2t2+t+1)、(t,t2+t﹣1),
则MN=(2t2+t+1)﹣(t2+t﹣1)=t2+2;
(3)①当∠ANM=90°时,AN=MN,
AN=t﹣(﹣2)=t+2,MN=t2+2,
t=t2+2,解得:t=0或1(舍去0),故t=1;
②当∠AMN=90°时,AM=MN,
AM=t+2=MN=t2+2,
解得:t=0或1(舍去1),故t=1;
综上,t=0或1.

练习册系列答案
相关题目