题目内容
在平面直角坐标系内，已知点A（2，2），B（2，-3），点P在y轴上，且△APB为直角三角形，则点P的个数为________．
4
分析：先在直角坐标平面内描出A、B两点，连接AB，因题设中未指明△APB的哪个角是直角，故应分别就∠A、∠B、∠C为直角来讨论，设点P（0，x），运用几何知识建立x的方程．即可求P的坐标．
解答：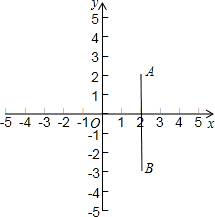
解：若∠A=90°，则P点（0，2）；
若∠B=90°，则P点（0，-3）；
若∠P=90°，则PA2+PB2=AB2，
而PA2=（2-x）2+22，
PB2=（x+3）2+22，
AB2=（2+3）2，
∴（2-x）2+22+（x+3）2+22=（2+3）2，
解得x=1或x=-2，
即P（0，1）或（0，-2）．
故在Y轴上的P点有4个．
故答案为：4．
点评：本题考查了平面直角坐标系中勾股定理的运用，考查了分类讨论思想，本题中根据勾股定理计算P点的纵坐标x是解题的关键．
分析：先在直角坐标平面内描出A、B两点，连接AB，因题设中未指明△APB的哪个角是直角，故应分别就∠A、∠B、∠C为直角来讨论，设点P（0，x），运用几何知识建立x的方程．即可求P的坐标．
解答：
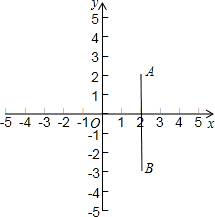解：若∠A=90°，则P点（0，2）；若∠B=90°，则P点（0，-3）；
若∠P=90°，则PA2+PB2=AB2，
而PA2=（2-x）2+22，
PB2=（x+3）2+22，
AB2=（2+3）2，
∴（2-x）2+22+（x+3）2+22=（2+3）2，
解得x=1或x=-2，
即P（0，1）或（0，-2）．
故在Y轴上的P点有4个．
故答案为：4．
点评：本题考查了平面直角坐标系中勾股定理的运用，考查了分类讨论思想，本题中根据勾股定理计算P点的纵坐标x是解题的关键．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
在平面直角坐标系内，已知点A（2，1），O为坐标原点．请你在坐标轴上确定点P，使得△AOP成为等腰三角形．在给出的坐标系中把所有这样的点P都找出来，画上实心点，并在旁边标上P1，P2，…，PK的坐标（有k个就标到PK为止，不必写出画法）．