题目内容
 在平面直角坐标系内,已知点A(2,1),O为坐标原点.请你在坐标轴上确定点P,使得△AOP成为等腰三角形.在给出的坐标系中把所有这样的点P都找出来,画上实心点,并在旁边标上P1,P2,…,PK的坐标(有k个就标到PK为止,不必写出画法).
在平面直角坐标系内,已知点A(2,1),O为坐标原点.请你在坐标轴上确定点P,使得△AOP成为等腰三角形.在给出的坐标系中把所有这样的点P都找出来,画上实心点,并在旁边标上P1,P2,…,PK的坐标(有k个就标到PK为止,不必写出画法).
分析:本题应先求出OA的长,再分别讨论OA=OP、AP=OA、AP=OP的各种情况,即可得出答案.
解答: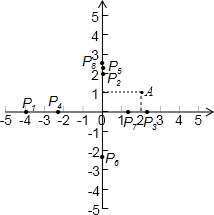 解:OA=
解:OA=
=
,OA=OP时,x轴上有(
,0),(-
,0);
y轴上有(0,
),(0,-
);
AP=OA时,x轴上有(4,0),y轴上(0,2);
AP=OP时,x轴上有(
,0)y轴上有(0,
)
∴p1(4,0),p2(0,2),p3(
,0),p4(-
,0),p5(0,
),p6(0,-
),p7(
,0),p8(0,
)
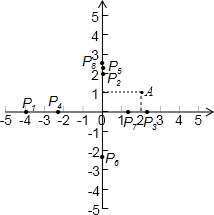 解:OA=
解:OA=| 12+22 |
| 5 |
| 5 |
| 5 |
y轴上有(0,
| 5 |
| 5 |
AP=OA时,x轴上有(4,0),y轴上(0,2);
AP=OP时,x轴上有(
| 5 |
| 4 |
| 5 |
| 2 |
∴p1(4,0),p2(0,2),p3(
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 4 |
| 5 |
| 2 |
点评:△AOP为等腰三角形,那么任意一对邻边可为等腰三角形,注意分情况讨论.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目